Machine Learning (Lee Hongyi)
ML framework:
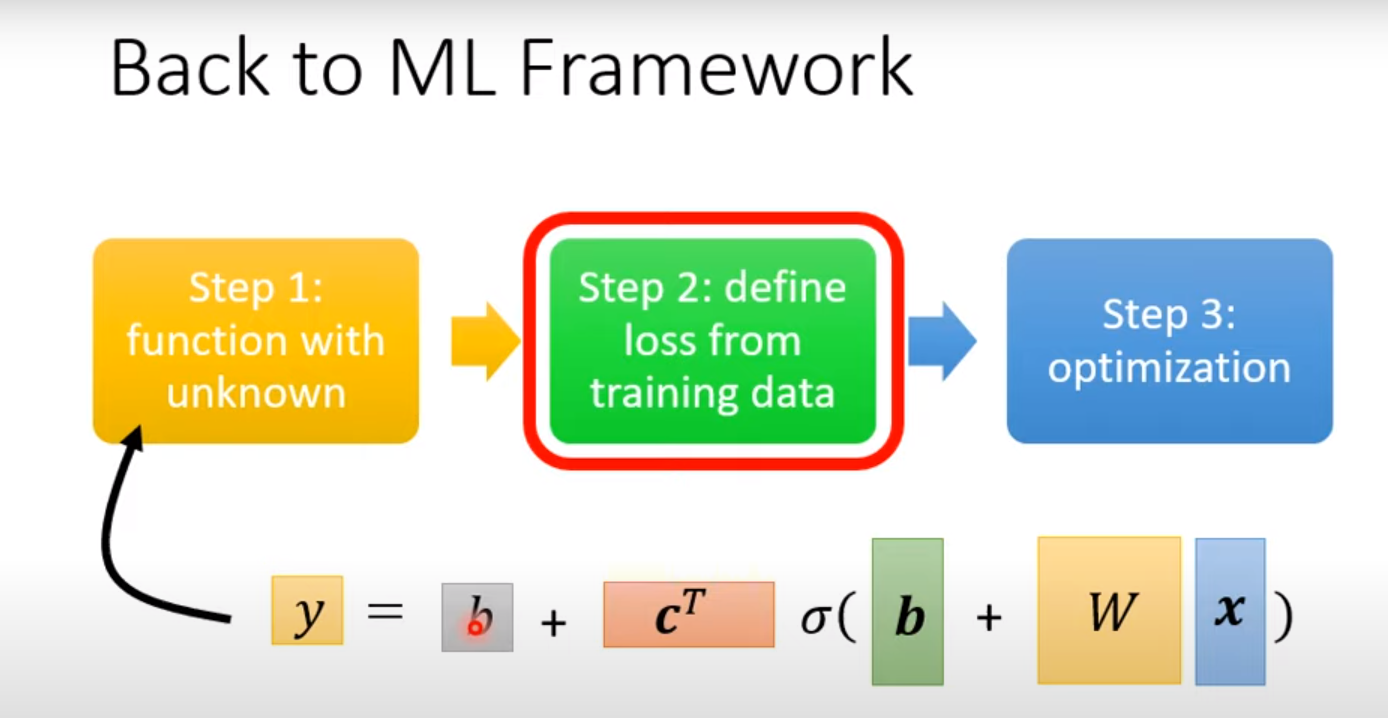
1. Function with unknown $y=f_\theta(x)$
Model bias:
Approximate continuous curve by a piecewise linear cure. In order to have good approximation, we need sufficient pieces (basic components of the piecewise linear curve).
sigmoid: $y(x;c,b,w)=c\frac{1}{1+e^{-(b+wx)}}$
How to reduce the model bias:
- more flexible model
- more feature
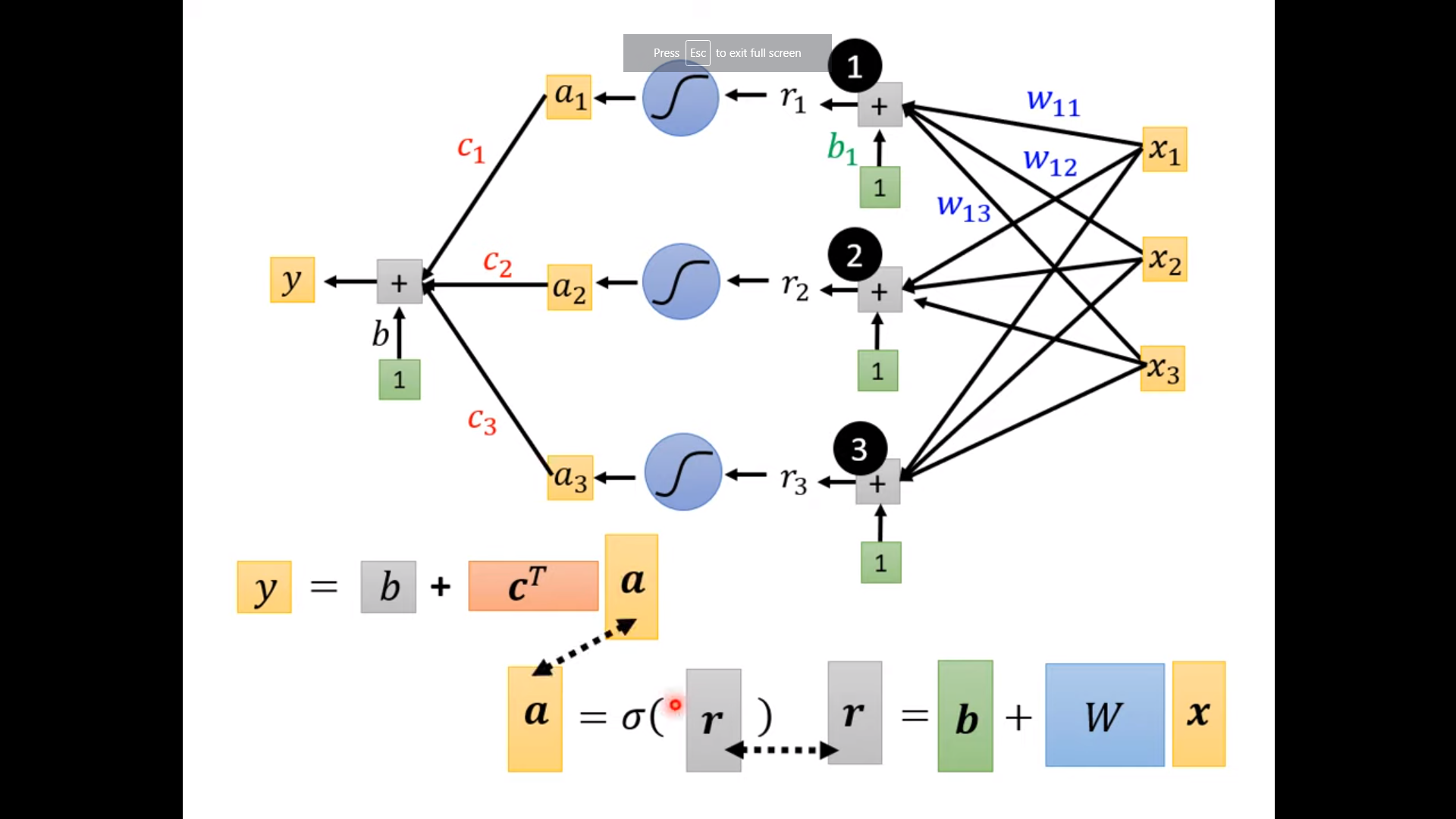
- In ML, the pieces (activation function) can be sigmoid function, hard sigmoid, ReLU, etc.
- number of hidden layer
2. Define Loss $L(\theta)$
Loss: function of parameters to evaluate how good of the set of parameters $L=\frac{1}{N} \sum_n e_n$.
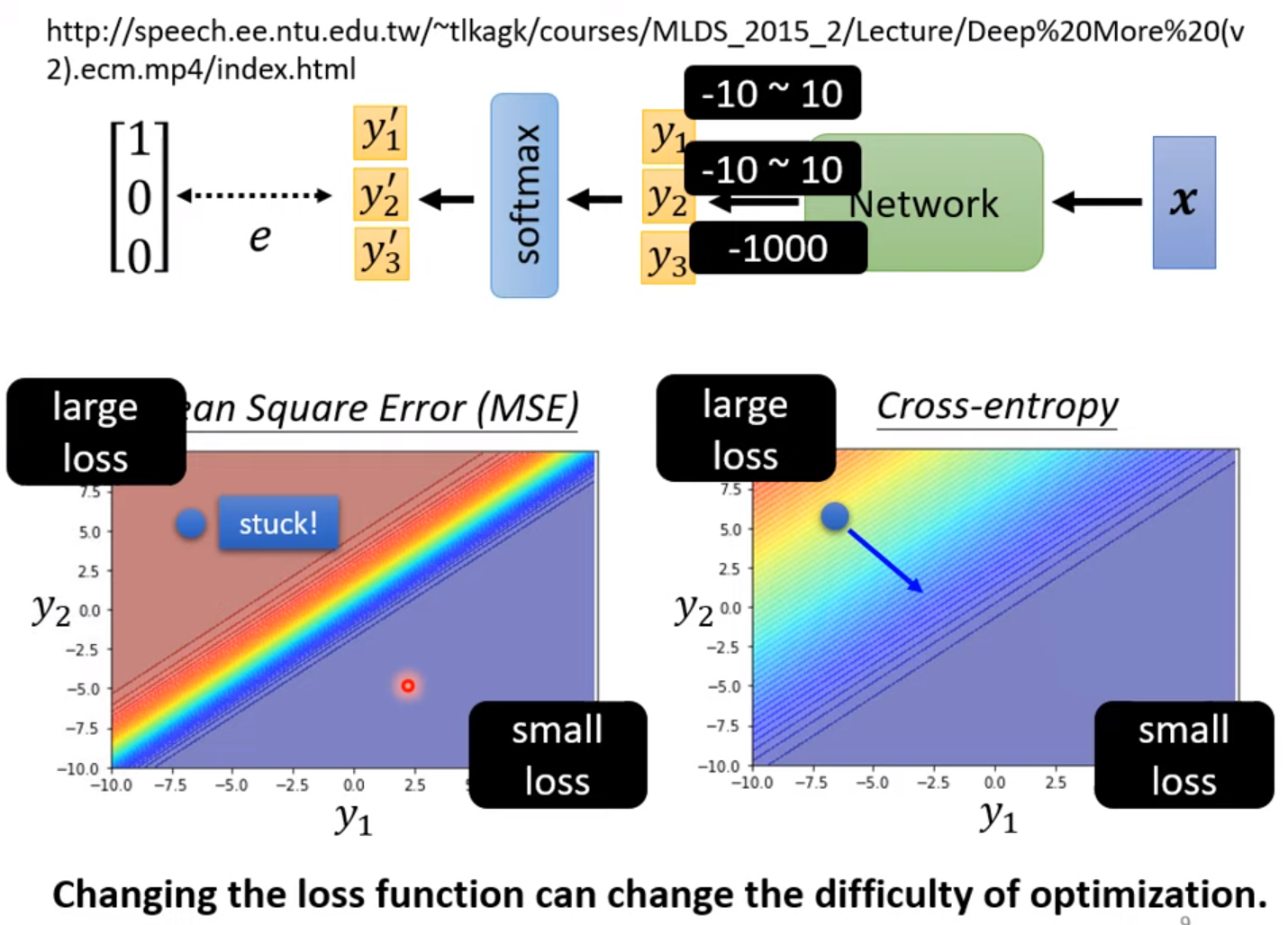
MAE, MSE, cross-entropy
cross-entropy: $e=-\sum_i \hat y_i \ln y_i’$ 其中, [$\hat y$ is label]
minimize cross-entropy is equivalent to maximizing likelihood.
3. Optimization: $\theta^* = \operatorname{argmin}_\theta L$
Gradient descent:

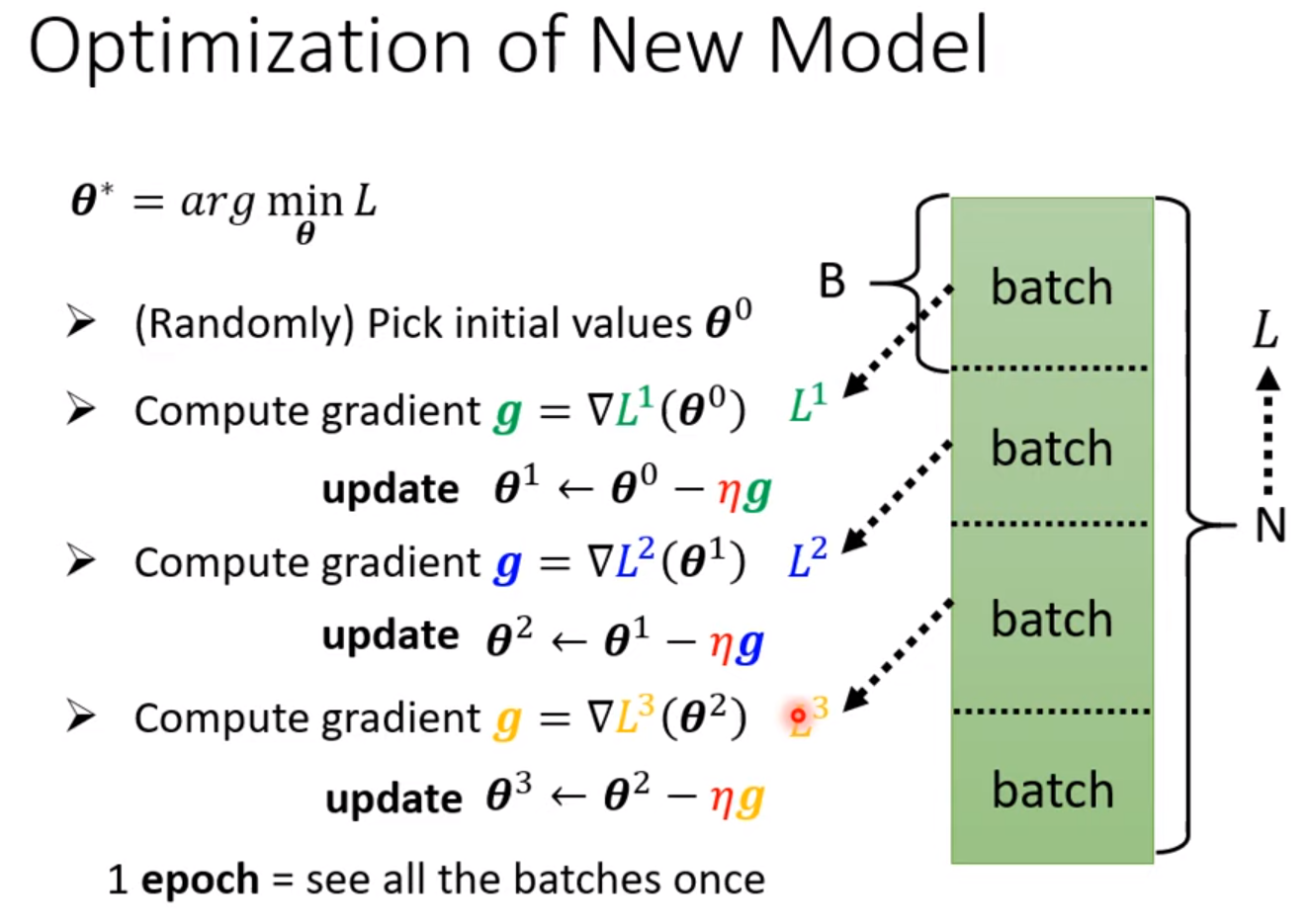
1个epoch之后,shuffle,改变batch
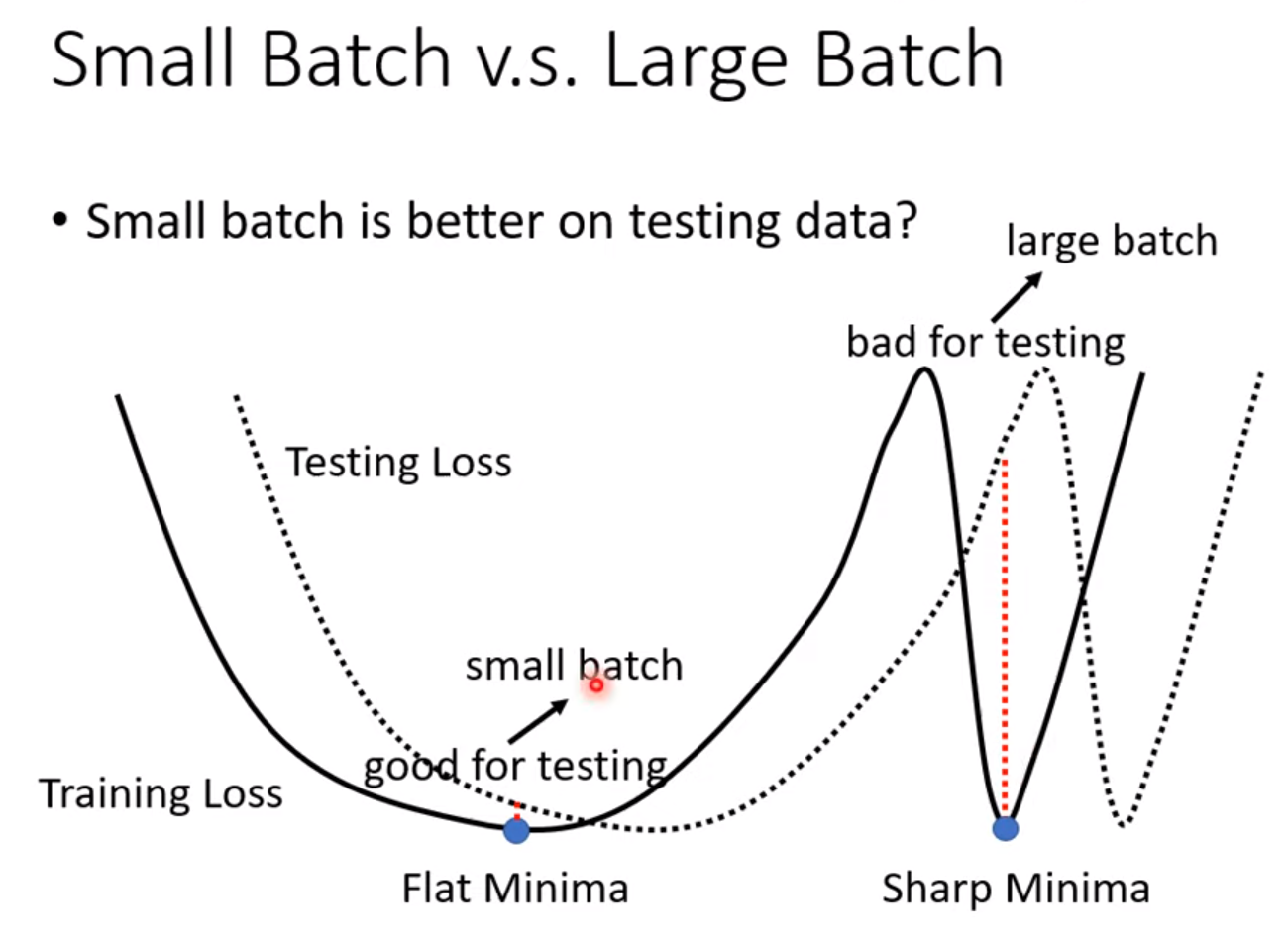
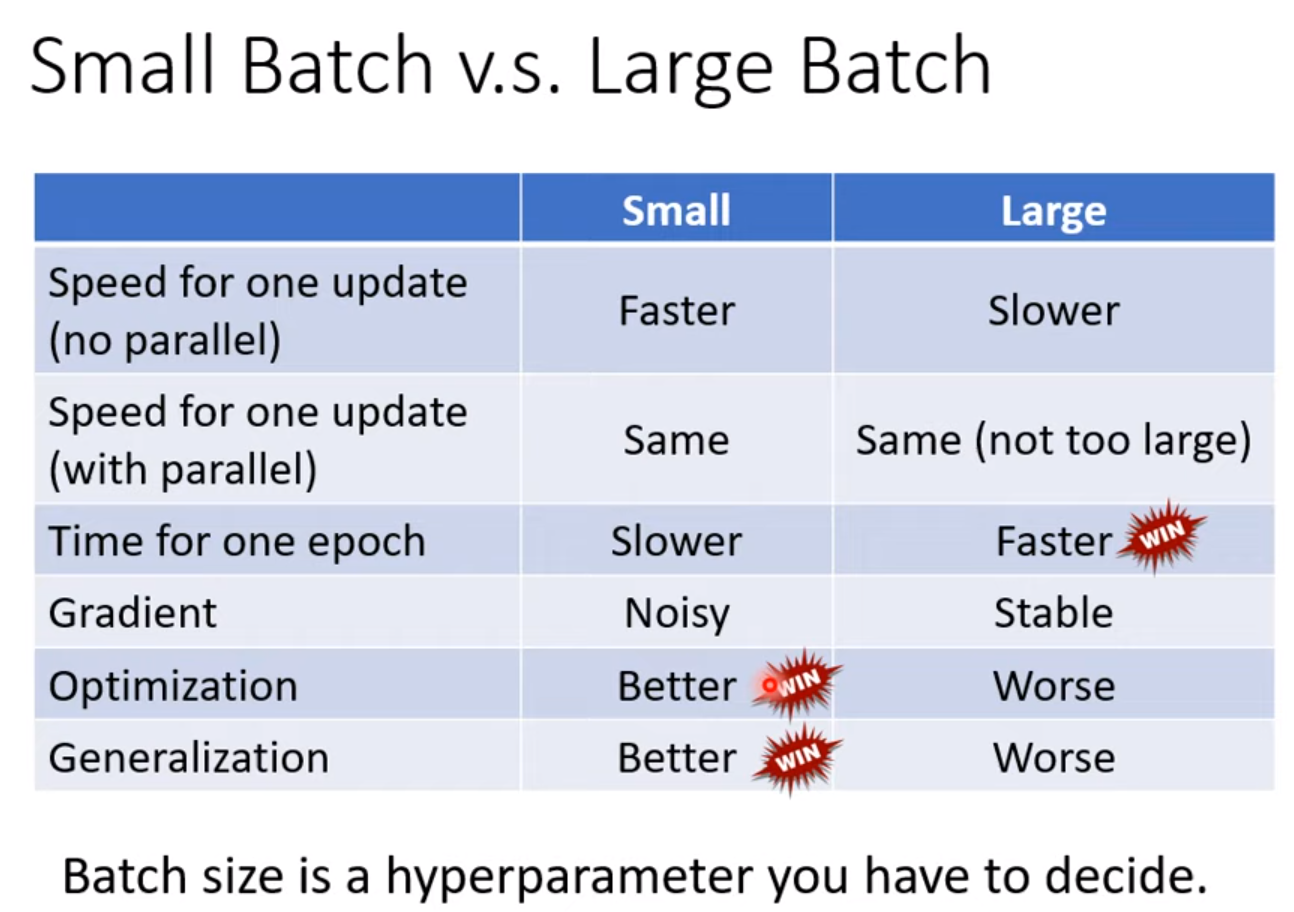
small batch v.s. large batch:
large batch (not too large) will not cost much time thanks to the GPU parallel computation. So, it will be efficient for one epoch
then small batch will cost much time for one epoch. It will result in noisy direction, which will be better in some cases.
large batch and small batch work well in training, but small batch works worse in testing – overfitting.
large batch and small batch work well in training, but large batch works worse in testing – NOT overfitting, 是因为optimization

Momentum [Consider direction]
Movement of last step - gradient at present
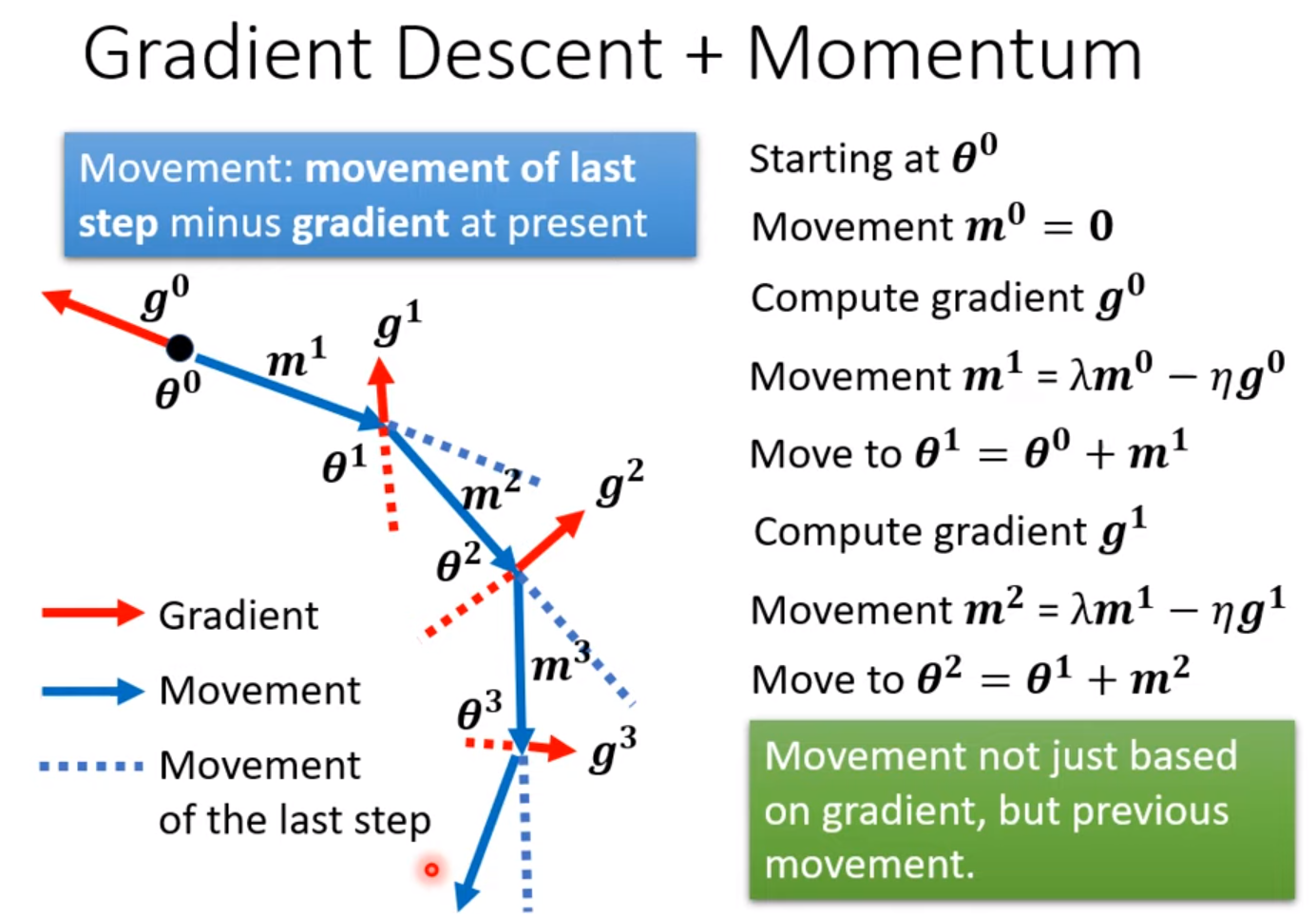
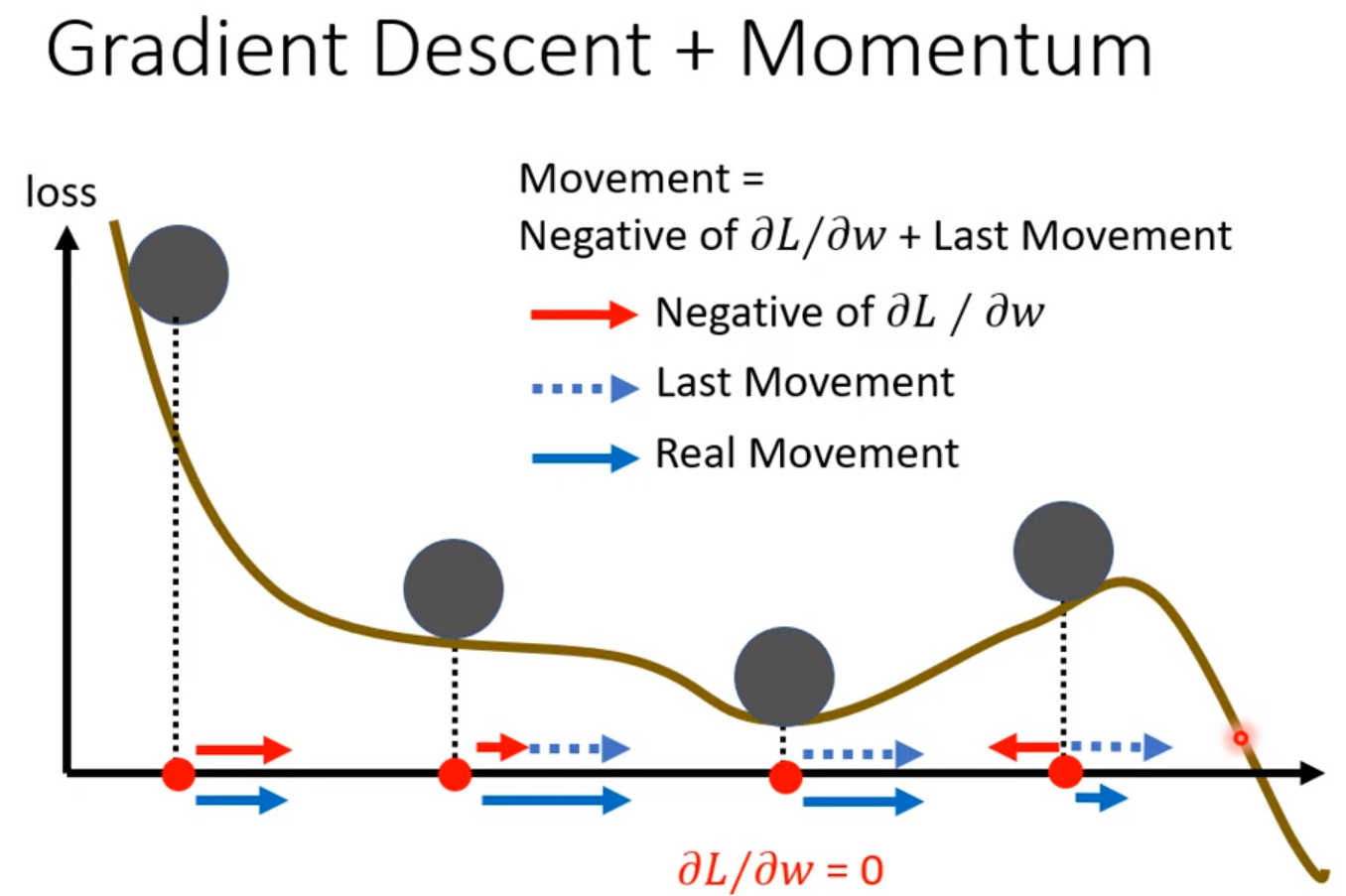
$m_i$ is the weighted sum of all the previous gradient $g^0, g^1, \cdots, g^{i-1}$.
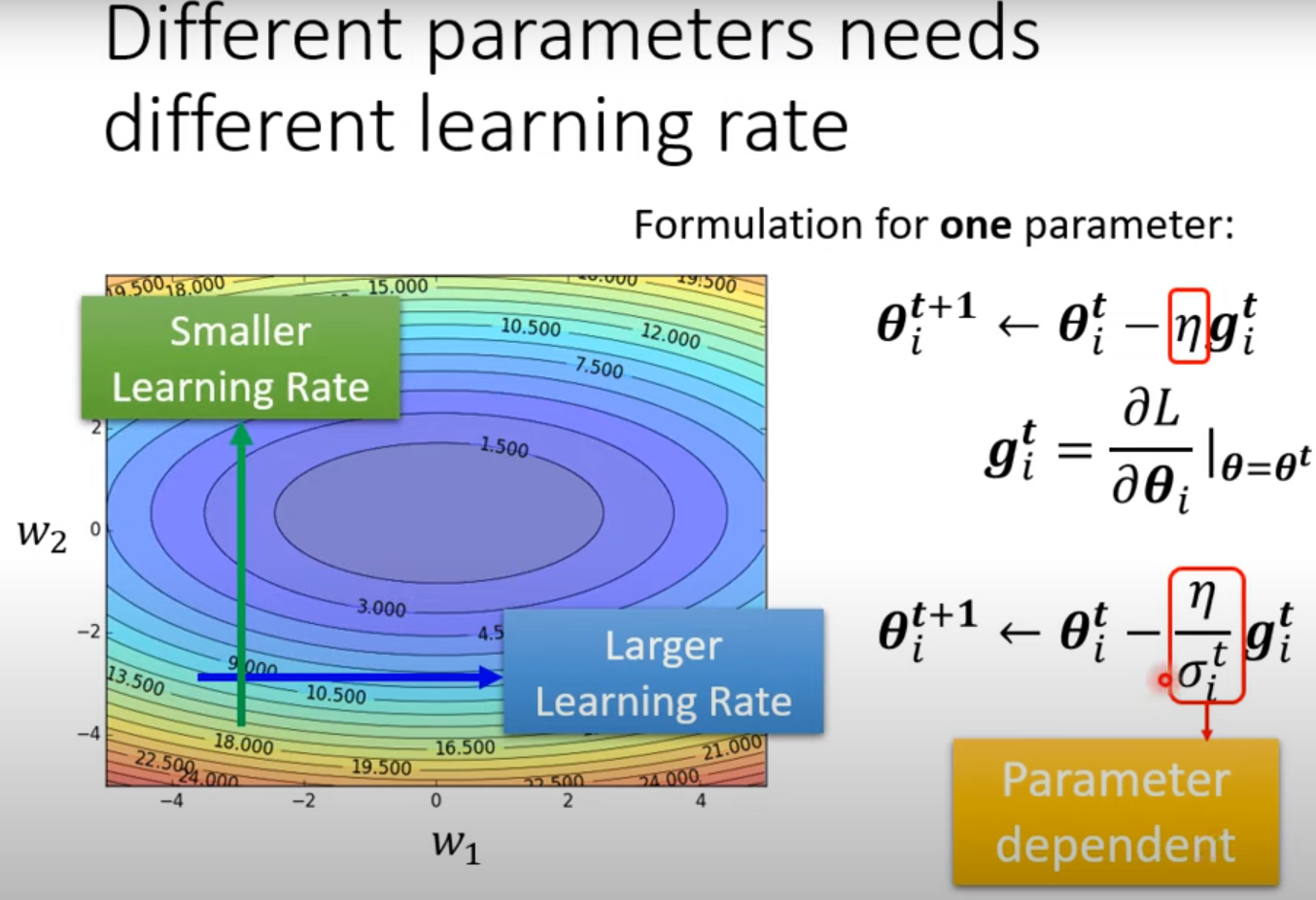
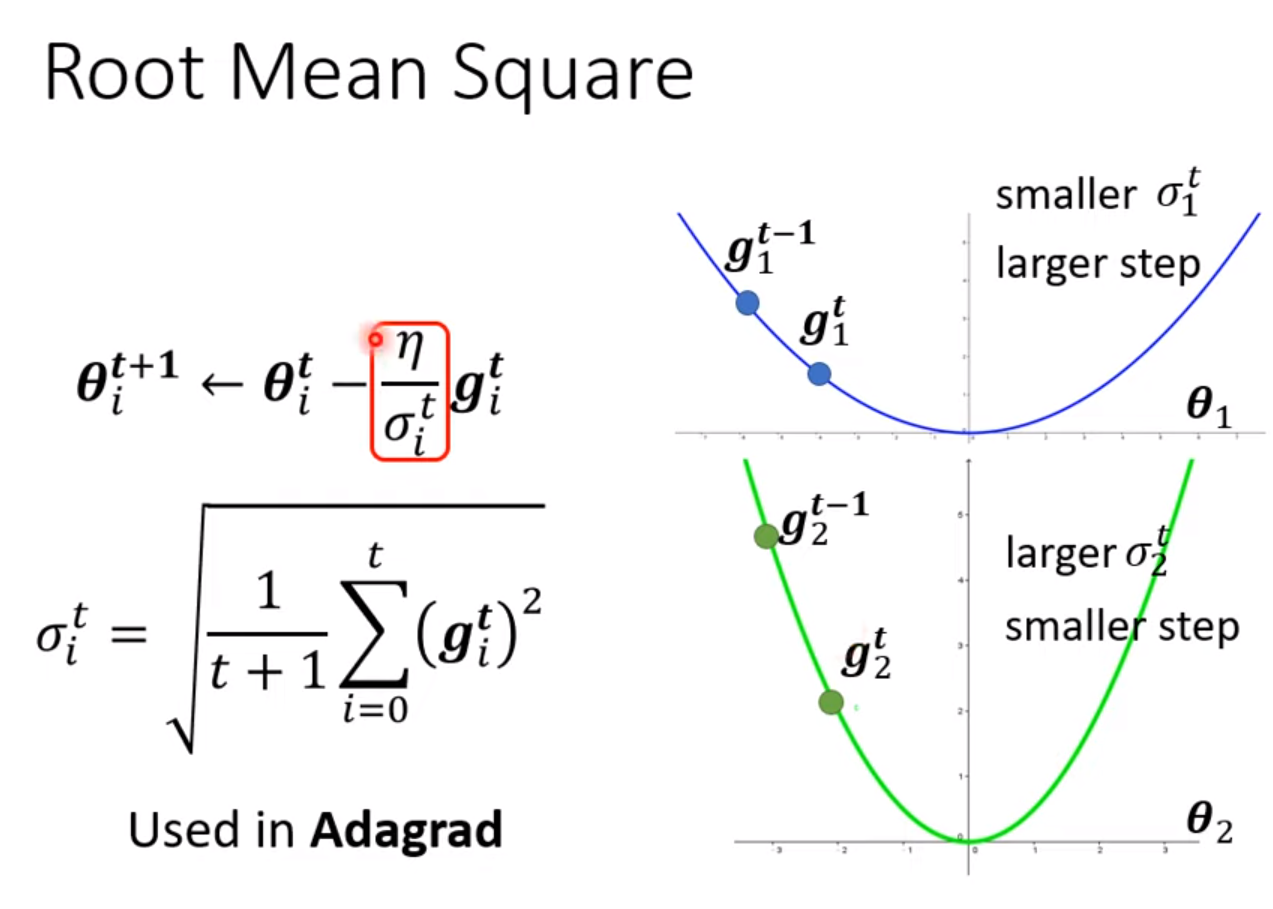
Adaptive learning rate [Consider magnitude]
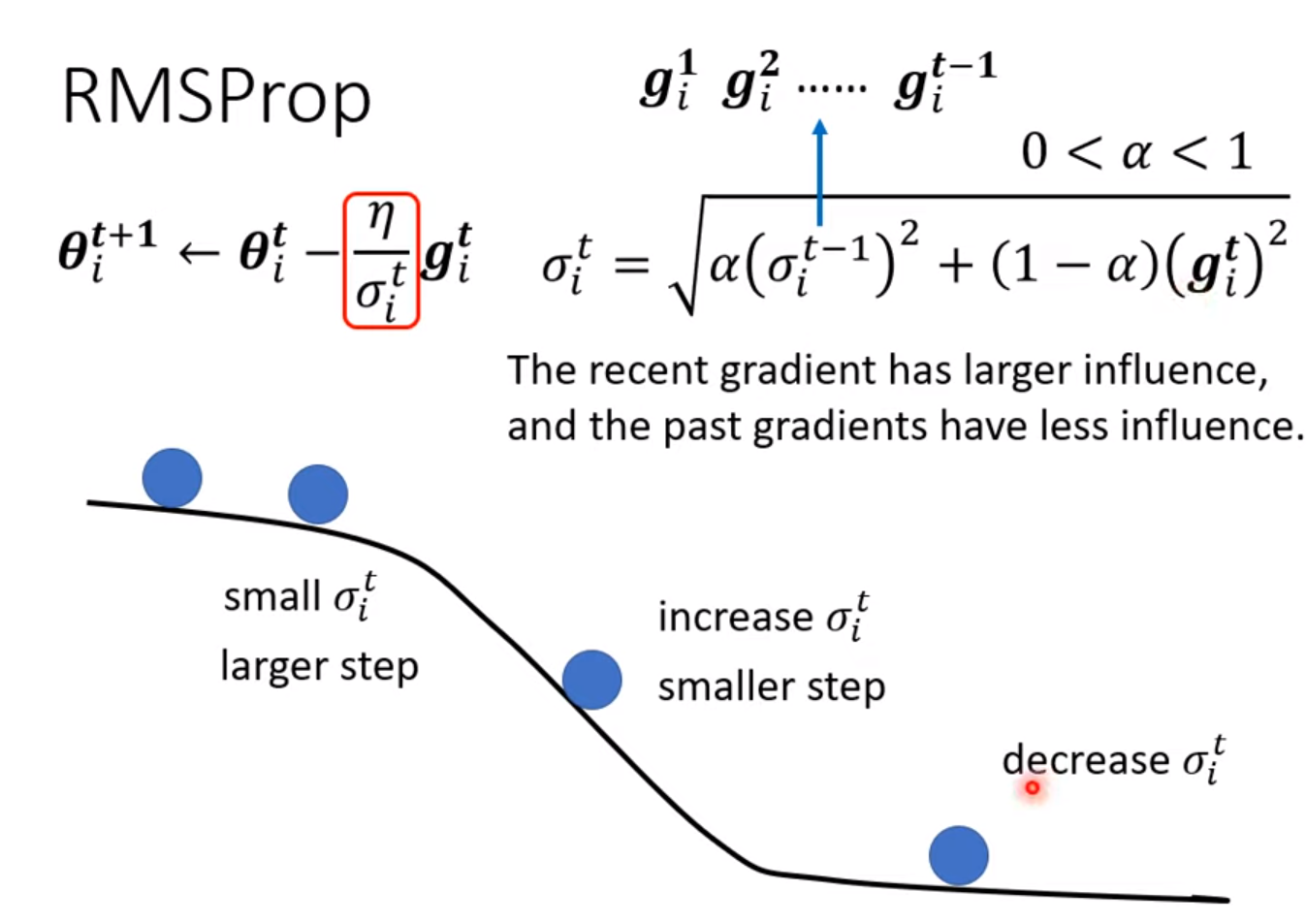
gradient 变化率小,选用大的learning rate;gradient 变化率大,选用小的learning rate。
- Adagrad
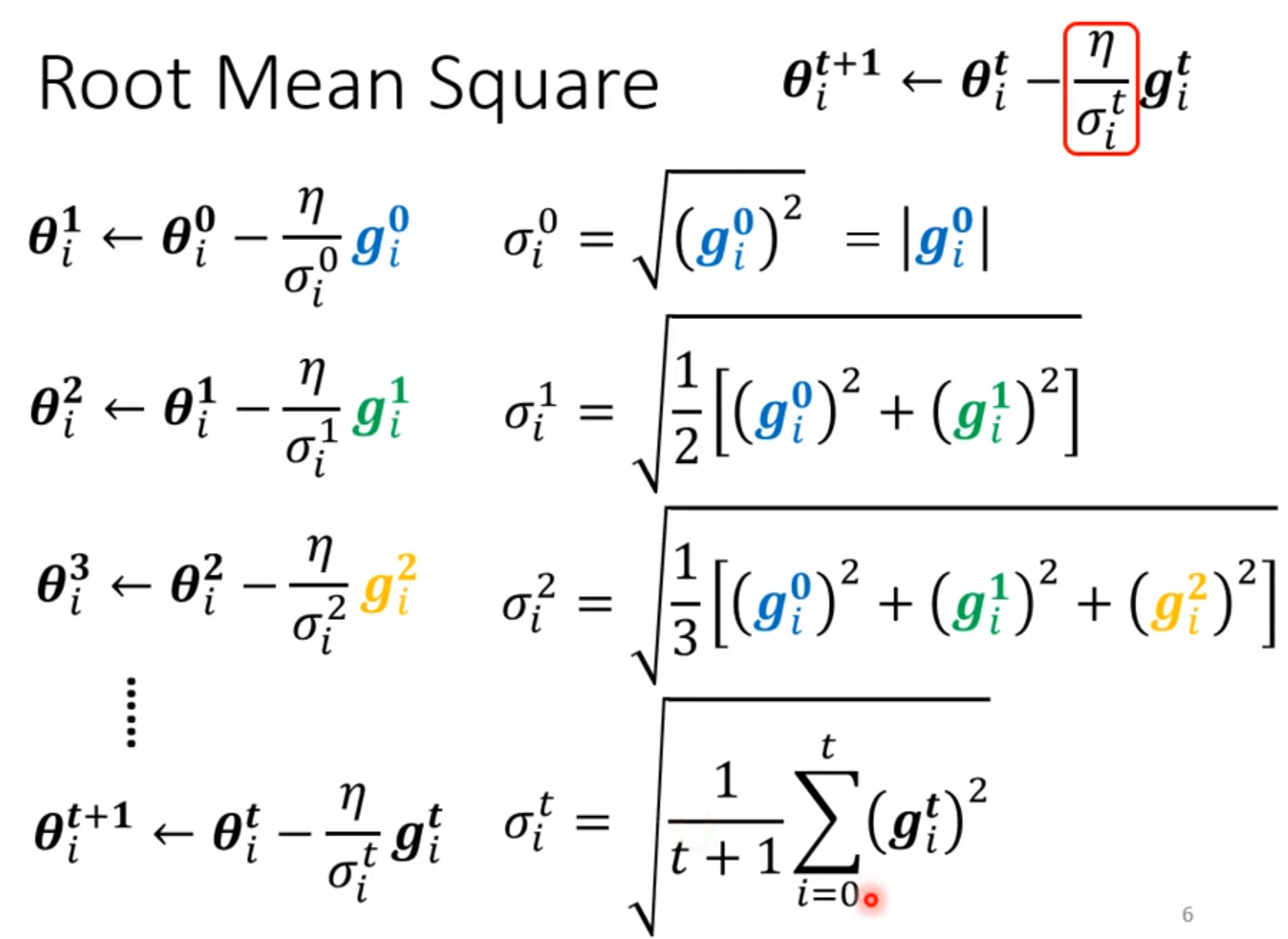
- RMSProp
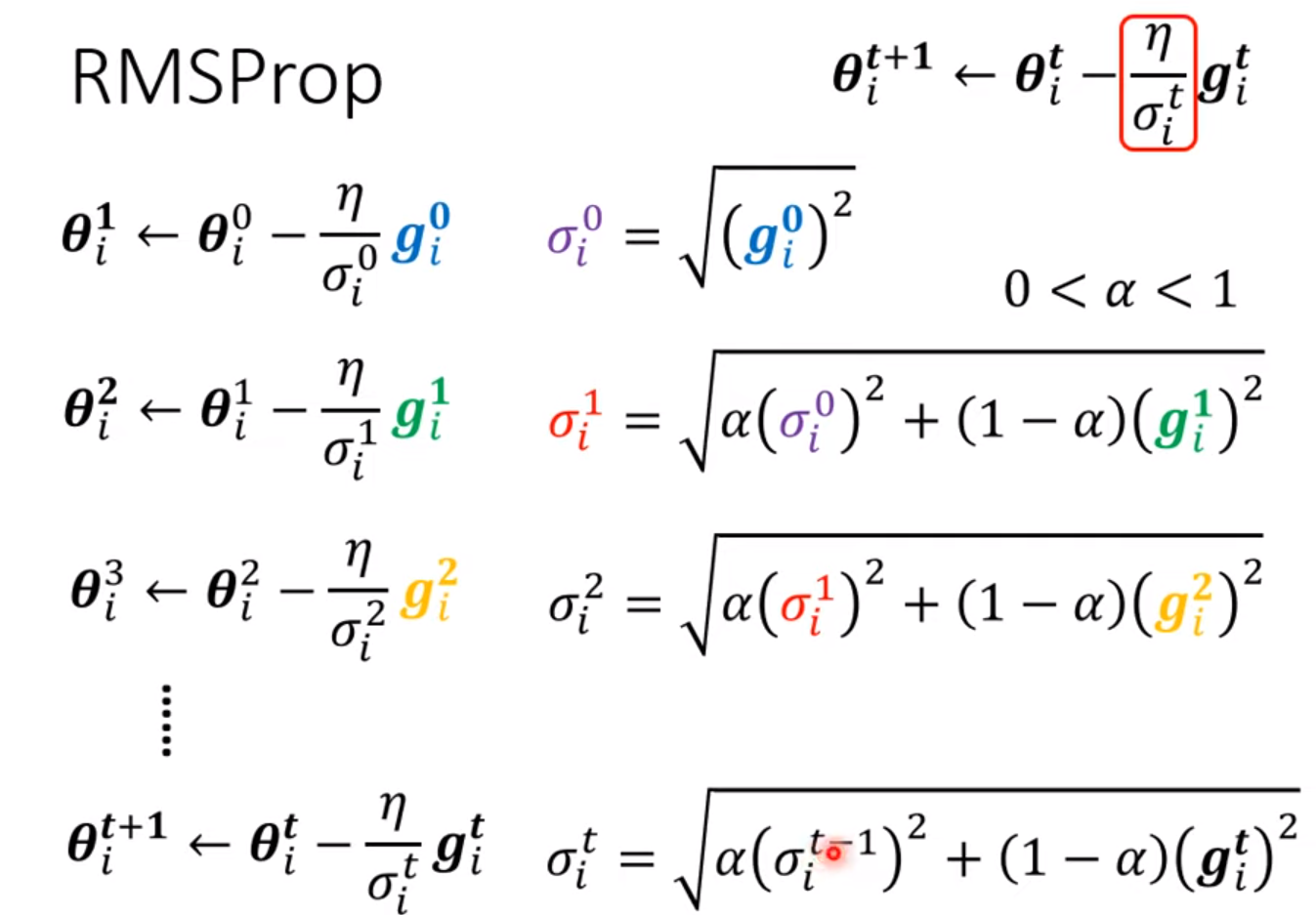
Adam: RMSProp + Momentum
Learning rate scheduling
- learning rate decay: As the time goes, we are closer to the destination, so we reduce the learning rate
- warm up: increase first and then decrease (at the beginning, the estimate of $\sigma_i^t$ has large variance) [RAdam]
Problem:
overfitting
Methods to improve:

reason of large loss on training data:
- Model bias: model is too simple. –> redesign more flexible model (more feature; more neutrons layers)
- Optimization: local minima
How to know which reason leads to the large loss on training data:
If deeper network has larger loss on training data, there might be optimization issue.


Overfitting:
Smaller loss on training data, and larger loss on testing data.
Solution:
- more training data;
- Data augmentation (reasonable);
- constrained model
- less parameters, sharing parameters [e.g. CNN which is constrained one compared with fully-connected NN]
- Less features
- early stopping
- regularization
- Dropout
But if give more constraints on model, –> Bias-complexity trade-off [cross validation, N-fold cross validation]

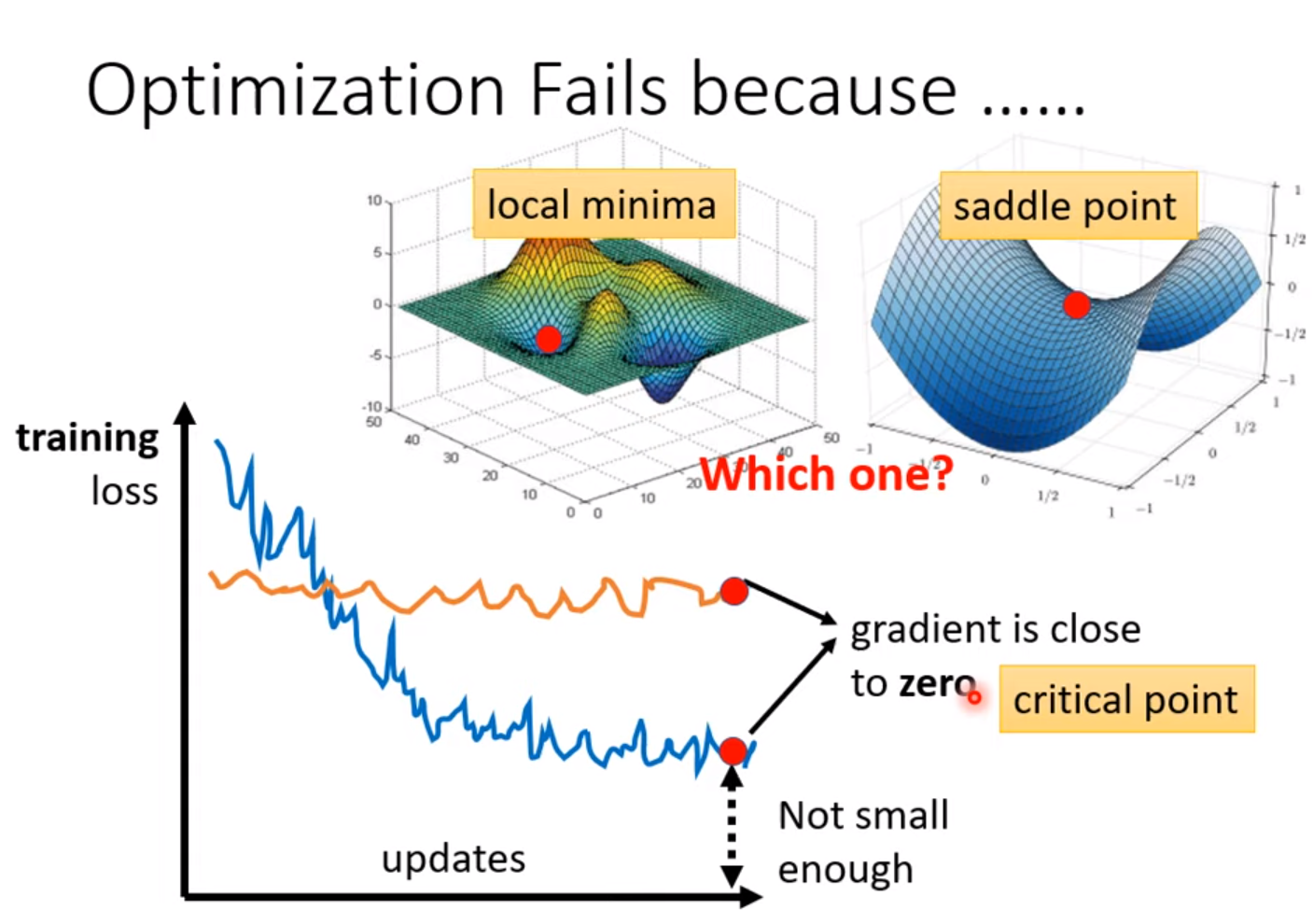
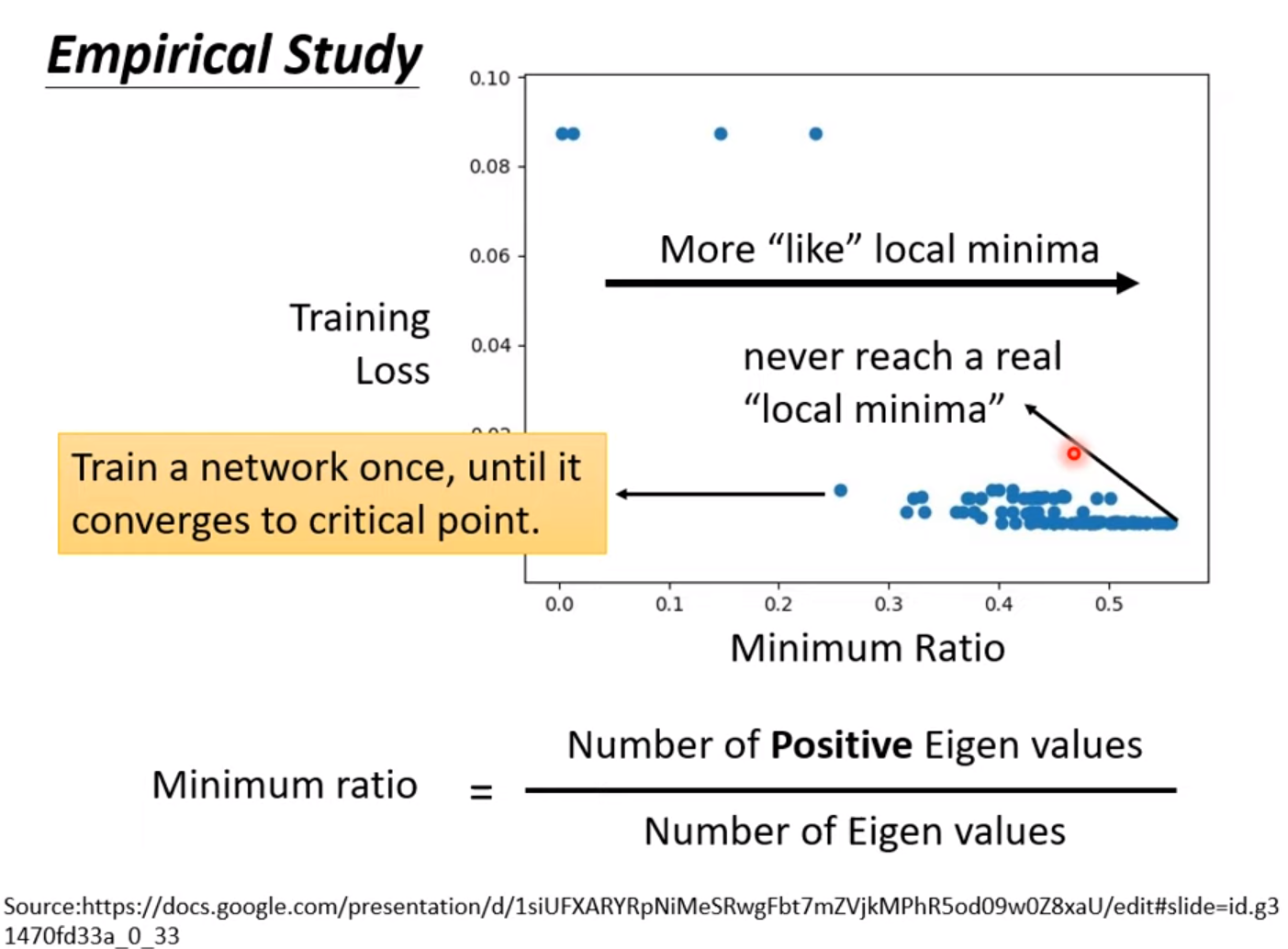
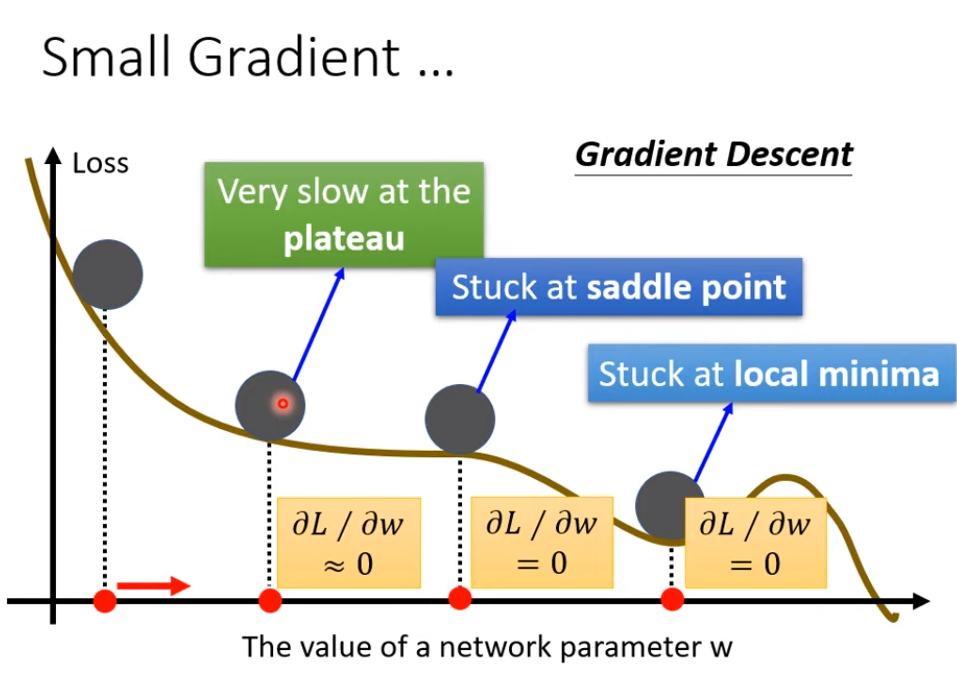
critical point: gradient = 0

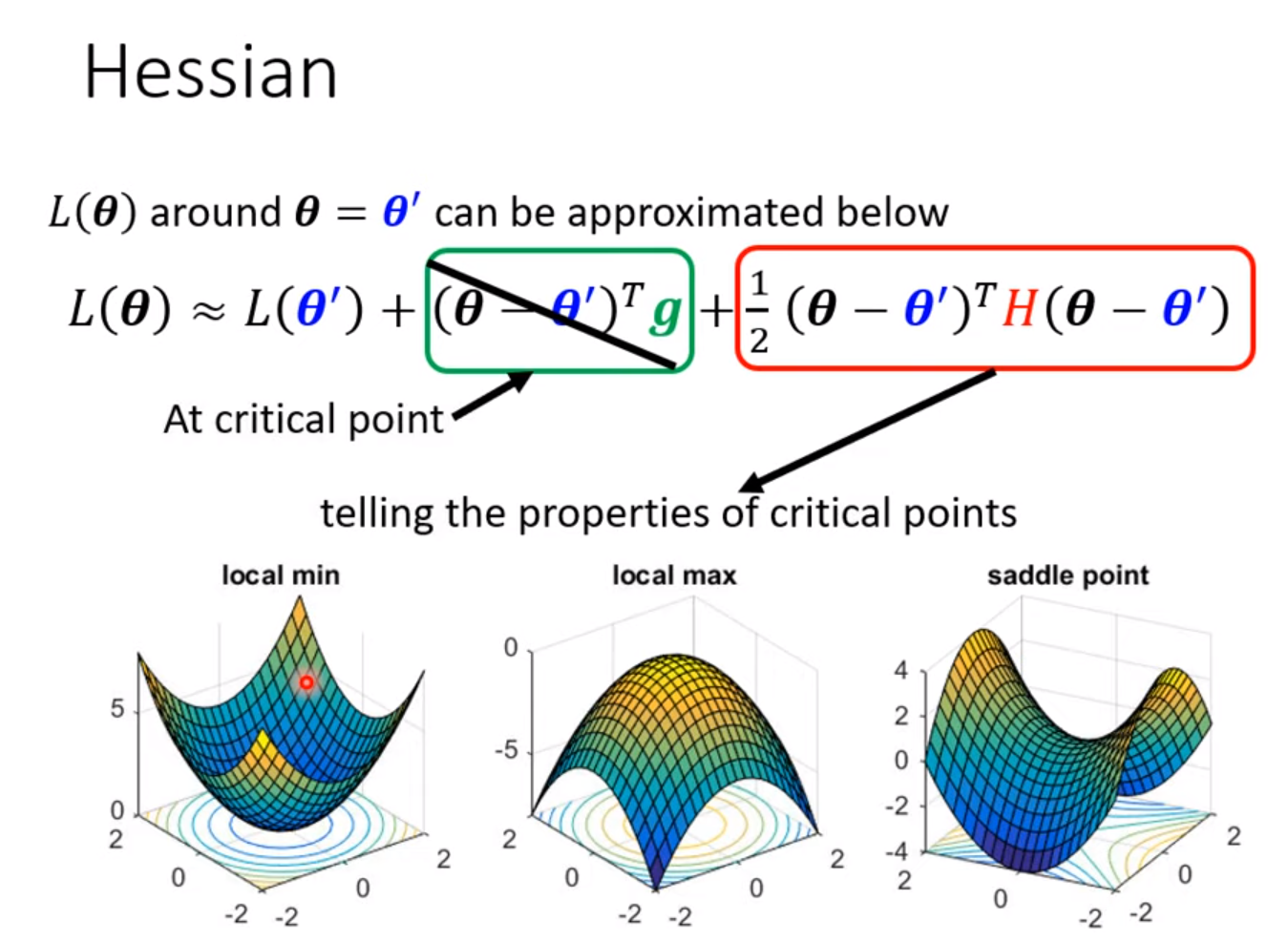

- 把data的loss写出来,求loss对每个参数的偏导,令其=0, 检测其Hessian
How to avoid critical point ?
Avoid saddle point

Based on eigenvector and eigenvalue of Hessian, we can update the parameter along the direction of the eigenvector –> reduce loss.
If enough more parameter, the error surface will be more complex. But the local minima will be degrade to saddle point. [local minima in low dimension –> saddle point in higher dimension].