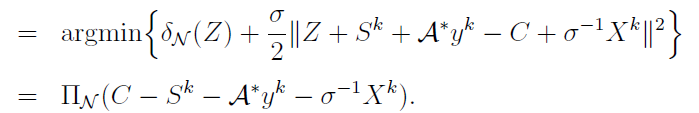Take form of decomposition-coordination procedure (solution of subproblem is coordinated to solution of global problem)
ADMM : bene�fits of dual decomposition + augmented Lagrangian methods for constrained optimization
0 precursor
0.1 Gradient Ascent
Primal problem
$$
\begin{array}{rc}
\min & f(x) \
\text{s.t.} & Ax=b
\end{array}
$$
Lagrangian function is
$$
L(x,y) = f(x) + y^T(Ax-b)
$$
and the dual function is
$$
g(y) = \inf_x L(x,y) = -f^*(-A^Ty) - b^Ty
$$
dual problem is
$$
\max g(y)
$$
recover a primal optimal point $x^*$ from a dual optimal point $y^*$
$$
x^* = \mathop{\mathrm{argmin}}x L(x,y^*)
$$
Solve this dual problem using gradient ascent:
$$
\begin{array}{rl}
x^{k+1} &=& \mathop{\mathrm{argmin}}{x} L(x,y^k) & x\text{-minimization step} \
y^{k+1} &=& y^k +\alpha^k(Ax^{k+1} - b) & \text{dual variable update}
\end{array}
$$
dual ascent method can lead to a decentralized algorithm in some case.
0.2 Dual Decomposition
If objective $f$ is separable,
$$
f(x) = \sum_{i=1}^N f_i(x_i), \text {where } x=(x_1, \cdots, x_N), \ A = [A_1, \cdots, A_N]
$$
the Lagrangian function is
$$
L(x,y) = \sum_{i=1}^N L_i(x_i,y) = \sum_{i=1}^N (f_i(x_i)+y^TA_ix_i - \frac{1}{N}(y^Tb)
$$
which is separable in $x$. This means that $x$-minimization step splits into $N$ separate problems that can be solved in parallel.
Solve:
$$
\begin{array}{rl}
x_i^{k+1} &=& \mathop{\mathrm{argmin}}_{x_i} L_i(x_i,y^k) & x_i\text{-minimization step} \
y^{k+1} &=& y^k +\alpha^k(Ax^{k+1} - b) & \text{dual variable update}
\end{array}
$$
So, the $x$-minimization step is carried out independently, in parallel.
**Each iteration of the dual decomposition requires a broadcast and gather operation **
[in dual update, collect $A_i x_i^{k+1}$ to compute the residual $Ax^{k+1}-b$. Once global dual variable $y^{k+1}$ is computed, it will be broadcast to $N$ individual $x_i$ minimization steps. ]
- [Book] Cooperative distributed multi-agent optimization (this book discusses dual decomposition methods and consensus problems).
- Distributed Dual Averaging in Networks (distributed methods for graph-structured optimization problems)
0.3 Augmented Lagrangians and Method of Multipliers
augmented lagrangian is to bring robustness to dual ascent method, and to yield convergence without assumptions like strict convexity or finiteness of $f$.
Augmented Lagrangian is
$$
L_\sigma(x,y) = f(x) + y^T(Ax-b) + \frac{\sigma}{2} |Ax-b|^2
$$
Dual function is
$$
g_\sigma(y) = \inf_x L_\sigma(x,y)
$$
Adding the penalty term is to be differentiable under rather mild conditions on the original problem.
find gradient of the augmented dual function by minimizing over $x$, then evaluating the resulting equality constraint residual.
Algorithm:
$$
\begin{array}{rl}
x^{k+1} &=& \mathop{\mathrm{argmin}}_{x} L_\sigma(x,y^k) & x\text{-minimization step} \
y^{k+1} &=& y^k +\sigma(Ax^{k+1} - b) & \text{dual variable update}
\end{array}
$$
Here, the parameter $\sigma$ is used as the step size $\alpha^k$.
[The method of multipliers converges under far more general conditions than dual ascent, including cases when $f$ takes on the value $+\infty$ or is not strictly convex.]
How to choose $\sigma$:
The optimality condition are primal and dual feasibility, i.e.,
$$
Ax^* - b = 0, \quad \nabla f(x^*) + A^Ty^* = 0
$$
Then, we have $x^{k+1}$ can minimize $L_\sigma(x,y^k)$, so
$$
\begin{aligned}
0 &= \nabla_x L_\sigma(x^{k+1}, y^k) \
&= \nabla_x f(x^{k+1}) + A^T(y^k + \sigma(Ax^{k+1}-b)) \
&= \nabla_x f(x^{k+1}) + A^T y^{k+1}
\end{aligned}
$$
So, using $\sigma$ as step size in dual update, the iterate $(x^{k+1}, y^{k+1})$ is dual feasible. $\rightarrow$ primal residual $Ax^{k+1}-b$ converges to 0. $\rightarrow$ optimality.
Shortcoming: When $f$ is separable, the augmented Lagrangian $L_\sigma$ is not separable, so the $x$-minimization step cannot be carried out separately in parallel for each $x_i$. This means that the basic method of multipliers cannot be used for decomposition
1. ADMM
blend the decomposability of dual ascent with the superior convergence properties of the method of multipliers.
Problem:
$$
\begin{array}{rcl}
\min & f(x)+g(z) \
\text{s.t. } & Ax+Bz = c
\end{array}
$$
difference: $x$ splits into two parts, $x$ and $z$, with the objective function separable across the splitting.
optimal value:
$$
p^* = \inf { f(x)+g(z) | Ax+Bz = c }
$$
Augmented Lagrangian:
$$
L_\sigma (x,z;y) = f(x)+g(z)+y^T(Ax+Bz-c)+\frac{\sigma}{2} |Ax+Bz-c|^2
$$
1.1 Algorithm
$$
\begin{aligned}
x^{k+1} &= \mathop{\mathrm{argmin}}_x L_\sigma(x,z^k,y^k) & x\text{-minimization}\
z^{k+1} &= \mathop{\mathrm{armmin}}_z L_\sigma(x^{k+1},z,y^k) & z\text{-minimization}\
y^{k+1} &= y^k + \sigma(Ax^{k+1}+Bz^{k+1}-c) & \text{dual variable update}
\end{aligned}
$$
why ADMM is alternating direction:
If use method of multipliers to solve this problem, we will have
$$
\begin{aligned}
(x^{k+1}, z^{k+1}) &= \mathop{\mathrm{argmin}}_{x,z} L_\sigma(x,z,y^k) \
y^{k+1} &= y^k + \sigma(Ax^{k+1}+Bz^{k+1}-c)
\end{aligned}
$$
So, the augmented lagrangian is minimized jointly with two variables $x,z$.
But, ADMM update $x$ and $z$ in an alternating or sequential fashion, –> alternating direction.
ADMM can be viewed as a version of method of multipliers where a single Gauss-Seidel pass over $x$ and $z$ is used instead of joint minimization.
combine the linear and quadratic terms in the augmented lagrangian and scale the residual variable.
Set $u = \frac{1}{\sigma} y$, the ADMM becomes
$$
\begin{array}{l}
{x^{k+1}:=\underset{x}{\operatorname{argmin}} \left(f(x) + \frac{\sigma}{2} \left|A x+B z^{k}-c+u^{k}\right|^{2}\right)} \
{z^{k+1}:=\underset{z}{\operatorname{argmin}} \left(g(z) + \frac{\sigma}{2} \left|A x^{k+1}+B z-c+u^{k}\right|^{2}\right)} \
{u^{k+1}:=u^{k}+A x^{k+1}+B z^{k+1}-c}\end{array}
$$
Define residual at $k$ iteration as $r^k=Ax^k+Bz^k-c$, we have
$$
u^k = u^0 + \sum_{j=1}^k r^j
$$
1.2 Convergence
Assumption 1:
function $f: \mathbb R^n \rightarrow \mathbb R \cup {+\infty}$ and $g: \mathbb R^m \rightarrow \mathbb R \cup {+\infty}$ are closed, proper and convex
this assumption means the subproblem in $x$-update and $z$-update are solvable.
allows $f$ and $g$ are nondifferentiable and to assume value $+\infty$. For example, $f$ is indicator function
Assumption 2:
Unaugmented Lagrangian $L_0$ has a saddle point. This means there exists $(x^*, z^*, y^*)$ such that
$$
L_0 (x^*, z^*, y) \leq L_0(x^*, z^*, y^*) \leq L_0(x^*, z^*, y^*)
$$
Based on assumption1, $L_0(x^*, z^*, y^*)$ is finite for saddle point $(x^*, z^*, y^*)$. So, $(x^*, z^*)$ is solution to $\mathrm{argmin}_{x,z} L(x,z,y)$. So, $Ax^* + Bz^* = c$ and $f(x^*)<\infty$, $g(z^*)<\infty$. =
It also implies that $y^*$ is dual optimal, and the optimal value of the primal and dual problem are equal, i.e., the strong duality holds.
Under Assumption 1 and Assumption 2, ADMM iteration satisfy:
- residual convergence: $r^k \rightarrow 0$ as $k\rightarrow \infty$.
- objective convergence: $f(x^k)+g(z^k) \rightarrow p^*$ as $k\rightarrow \infty$.
- dual variable convergence: $y^k \rightarrow y^*$ as $k\rightarrow \infty$.
1.3 Optimality condition and Stopping creterion
1.3.1 Optimality condition for ADMM:
- Primal feasibility
$$
Ax^* + Bz^* -c = 0
$$
- Dual feasibility
$$
\begin{aligned}
0 &\in \part f(x^*) + A^Ty^* \
0 &\in \part g(z^*) + B^Ty^*
\end{aligned}
$$
Since $z^{k+1}$ minimizes $L_\sigma(x^{k+1},z,y^k)$, we have
$$
0\in \part g(z^{k+1}) + B^T y^k + \sigma B^T(Ax^{k+1}+Bz^{k+1}-c)\
= \part g(z^{k+1}) + B^T y^k + \sigma B^T r^{k+1} \
= \part g(z^{k+1}) + B^T y^k
$$
This means that $z^{k+1}$ and $y^{k+1}$ satisfy $0\in \part g(z^*)+ B^T u^*$. Similarly, can obtain other conditions.
the last condition holds for $(x^{k+1}, z^{k+1}, y^{k+1})$, the residual for the other two are primal and dual residuals $r^{k+1}$ and $s^{k+1}$.
1.3.2 Stopping criteria
suboptimality
$$
f(x^k)+g(z^k)-p^* \leq -(y^k)^Tr^k + (x^k-x^*)^T s^k
$$
shows that when the residuals $r^k$ and $s^k$ are small, the objective suboptimality will be small.
It’s hard to use this inequality as stopping criterion. But if we guess $|x^k-x^* | \leq d$, we have
$$
f(x^k)+g(z^k)-p^* \leq -(y^k)^Tr^k + d |s^k| \leq |y^k| |r^k| + d|s^k|
$$
so, the stopping criterion is that the primal and dual residual are small, i.e.,
$$
|r^k| \leq \epsilon^{\mathrm {pri}} \quad \text{and } \quad |s^k| \leq \epsilon^{\text{dual}}
$$
where $\epsilon^{\text{pri}}, \epsilon^{\text{dual}}$ are feasibility tolerance for primal and dual feasibility conditions. These tolerance can be chosen using an absolute and relative criterion, such as
$$
\begin{aligned}
\epsilon^{\text{pri}} &= \sqrt{p} \epsilon^{\text{abs}} + \epsilon^{\text{rel}} \max{ |Ax^k|, B|z^k|, |c| }, \
\epsilon^{\text{dual}} &= \sqrt{n} \epsilon^{\text{abs}} + \epsilon^{rel} |A^Ty^k|
\end{aligned}
$$
1.4 Extension and Variations
Varying Penalty Parameter
using different penalty parameters $\sigma^k$ for each iteration. -> improve convergence, reduce independence on initial $\sigma$.
$$
\sigma^{k+1}:=\left{\begin{array}{ll}
{\tau^{\text {incr }} \sigma^{k}} & {\text{if } |r^{k}| > \mu |s^{k}|} \
{\sigma^{k} / \tau^{\text {decr }}} & {\text {if }|s^{k}| > \mu |r^{k}|} \
{\sigma^{k}} & {\text { otherwise }}
\end{array}\right.
$$
where $\mu>1, \tau^{\text{incr}}>1, \tau^{\text{decr}}>1$ are parameters.
The idea behind this penalty parameter update is to try to keep the primal and dual residual norms within a factor of $\mu$ of one another as they both converge to zero.
large values of $\sigma$ place a large penalty on violations of primal feasibility and so tend to produce small primal residuals.
Conversely, small values of $\sigma$ tend to reduce the dual residual, but at the expense of reducing the penalty on primal feasibility, which may result in a larger primal residual.
So, when primal residual becomes large, inflates $\sigma$ by $\tau^{\text{incr}}$; when primal residual seems too small, deflates $\sigma$ by $\tau^{\text{decr}}$.
When a varying penalty parameter is used in the scaled form of ADMM, the scaled dual variable $u^k=\frac{1}{\sigma} y^k$ should be rescaled after updating $\sigma$.
More general Augmenting terms
- idea 1: use different penalty parameters for each constraint,
- idea 2: replace the quadratic term $\frac{\sigma}{2} |r|^2$ with $\frac{1}{2} r^TPr$, where $P$ is a symmetric positive definite matrix.
Over-relaxation in the $z$- and $y$- updates, $Ax^{k+1}$ can be replaced with
$$
\alpha^k Ax^{k+1} - (1-\alpha^k) (Bz^k-c)
$$
where $\alpha^k \in (0,2)$ is a relaxation parameter. When $\alpha^k >1$, over-relaxation; when $\alpha^k<1$, under-relaxation.
Inexact minimization
ADMM will converge even when the $x$- and $z$-minimization steps are not carried out exactly, provided certain suboptimality measures in the minimizations satisfy an appropriate condition, such as being summable.
in situations where the x- or z-updates are carried out using an iterative method; it allows us to solve the minimizations only approximately at first, and then more accurately as the iterations progress
Update ordering
$x$-, $y$-, $z$- updates in varying orders or multiple times.
for example:
divide variables into $k$ blocks and update each of them in turn (multiple times). –> multiple Gauss-Seidel passes.
Related algorithms
Dual ADMM [80]: applied ADMM to a dual problem.
Distributed ADMM [183]:
combination ADMM and proximal method of multipliers.
2. General Patterns
Three cases:
- quadratic objective terms;
- separable objective and constraints;
- smooth objective terms.
Here, we just discuss $x$-update, and can be easily applied to $z$-update.
$$
x^+ = \mathop{\mathrm{argmin}}_x (f(x)+\frac{\sigma}{2} |Ax-v|^2)
$$
where $v=-Bz+c-u$ is a known constant vector for the purpose of the $x$-update.
2.1 Proximity Operator
If $A=I$, $x$-update is
$$
x^+ = \mathop{\mathrm{argmin}}x (f(x)+\frac{\sigma}{2} |x-v|^2) = \mathrm{Prox}{f,\sigma}(v)
$$
Moreau envelope or MY regularization of $f$:
$$
\tilde f(v) = \inf_x (f(x)+\frac{\sigma}{2} |x-v|^2 )
$$
So, the $x$-minimization in the proximity operator is called proximal minimization.
for example: if $f$ is the indicator function of set $\mathcal C$, the $x$-update is
$$
x^+ = \mathop{\mathrm{argmin}}x (f(x)+\frac{\sigma}{2} |x-v|^2) = \Pi{\mathcal C}(v)
$$
2.2 Quadratic Objective Terms
$$
f(x) = \frac{1}{2} x^TPx+q^Tx+r
$$
where $P\in \mathbb S^n_+$, the set of symmetric positive semidefinite $n\times n$ matrices.
Assume $P+\sigma A^TA$ is invertible, $x^+$ is an affine function of $v$ given by
$$
x^+ = (P+\sigma A^TA)^{-1} (\sigma A^Tv-q)
$$
direct methods:
If we want to solve $Fx=g$, steps:
factoring $F = F_1F_2\cdots F_k$
back-solve: solve $F_iz_i=z_{i-1}$ where $z_1=F_1^{-1}g$ and $x=z_k$
(given $z_1$, can compute $z_2$ based on $F_2z_2 =z_1$, then iterates, so can compute $z_k$, i.e., can compute $x$).
The cost of solving $Fx = g$ is the sum of the cost of factoring $F$ and the cost of the back-solve.
In our case, $F=P+\sigma A^TA, \ g=\sigma A^Tv-q$, where $P\in \mathbb S_+^n, A\in \mathbb R^{p\times n}$.
We can form $F = P + \sigma A^TA$ at a cost of $O(pn^2)$ flops (floating point operations). We then carry out a Cholesky factorization of $F$ at a cost of $O(n^3)$ flops; the back-solve cost is $O(n^2)$. (The cost of forming $g$ is negligible compared to the costs listed above.) When $p$ is on the order of, or more than $n$, the overall cost is $O(pn^2)$. (When $p$ is less than $n$ in order, the matrix inversion lemma described below can be used to carry out the update in $O(p^2n)$ flops.)
Exploiting Sparsity
When $A$ and $P$ can make $F$ sparse. can be more efficient
Caching Factorizations
$Fx^{(i)}=g^{(i)}$, If $t$ is the factorization cost and $s$ is the back-solve cost, then the total cost becomes $t + Ns$ instead of $N(t + s)$, which would be the cost if we were to factor $F$ each iteration. As long as $\sigma$ does not change, we can factor $P + \sigma A^TA$ once, and then use this cached factorization in subsequent solve steps
Matrix Inversion Lemma
$$
\left(P+\sigma A^{T} A\right)^{-1}=P^{-1}-\sigma P^{-1} A^{T}\left(I+\sigma A P^{-1} A^{T}\right)^{-1} A P^{-1}
$$
For efficient computation.
Quadratic Function restricted to an Affine Set
$$
f(x)=(1 / 2) x^{T} P x+q^{T} x+r, \quad \text { dom } f={x | F x=g}
$$
Here, $x^+$ is still an affine function of $v$. the update involves solving the KKT condition:
$$
\left[\begin{array}{cc}{P+\sigma I} & {F^{T}} \ {F} & {0}\end{array}\right]\left[\begin{array}{c}{x^{k+1}} \ {\nu}\end{array}\right]+\left[\begin{array}{c}{q-\sigma\left(z^{k}-u^{k}\right)} \ {-g}\end{array}\right]=0
$$
==So, here, A=I?==
2.3 Smooth Objective Terms
If $f$ is smooth, can use iterative methods. (gradient method, nonlinear conjugate gradient, L-BFGS)
The convergence of these methods depends on the conditioning of the function to be minimized. The presence of the quadratic penalty term $\frac{\sigma}{2} |Ax-v|^2$ tends to improve the conditioning of the problem and thus improve the performance of an iterative method for updating $x$.
Can adjust $\sigma$ in each iteration to converges quichly.
Early Termination
Early termination in the $x$- or $z$-updates can result in more ADMM iterations, but much lower cost per iteration, giving an overall improvement in efficiency.
Warm Start
initialize the iterative method used in the $x$-update at the solution $x^k$ obtained in the previous iteration
Quadratic Objective Terms
worth using an iterative method than a direct method. –> conjugate gradient method.
Can use when direct method do not work, or $A$ is dense.
2.4 Decomposition
Block Separability
$x=(x_1, \cdots, x_N)$, then $f(x)=f_1(x_1) + \cdots +f_N(x_N)$. If the quadratic term $|Ax|^2$ is also separable, i.e., $A^TA$ is block diagonal, then the augmented lagrangian $L_\sigma$ is separable. –> compute in parallel.
Component separability
$f(x)=f_1(x_1) + \cdots +f_n(x_n)$ and $A^TA$ is diagonal. $x$-minimization step can be carried out via $n$ scalar minimization.
Soft Thresholding
If $f(x)=\lambda ||x|1$ and $A=I$, –> component separability. the scalar $x_i$-update is
$$
x_i^+ = \mathop{\operatorname{argmin}}{x_i}(\lambda |x_i| + \frac{\sigma}{2}(x_i-v_i)^2)
$$
Even the first term is not differentiable, But can use subdifferential.
$$
\begin{array}{ll}
&x_i^+ = S_{\frac{\lambda}{\sigma}} (v_i)& \
\text{where }& & \
&S_\kappa(a) = \begin{cases} a-\kappa,\quad& a>\kappa \ 0, \quad& |a|\leq \kappa \
a+\kappa, \quad& a< -\kappa\end{cases} \text{ or } S_\kappa(a) = (a-\kappa)- - (-a-\kappa)+
\end{array}
$$
Actually, this is proximity operator of the $\ell_1$ norm.
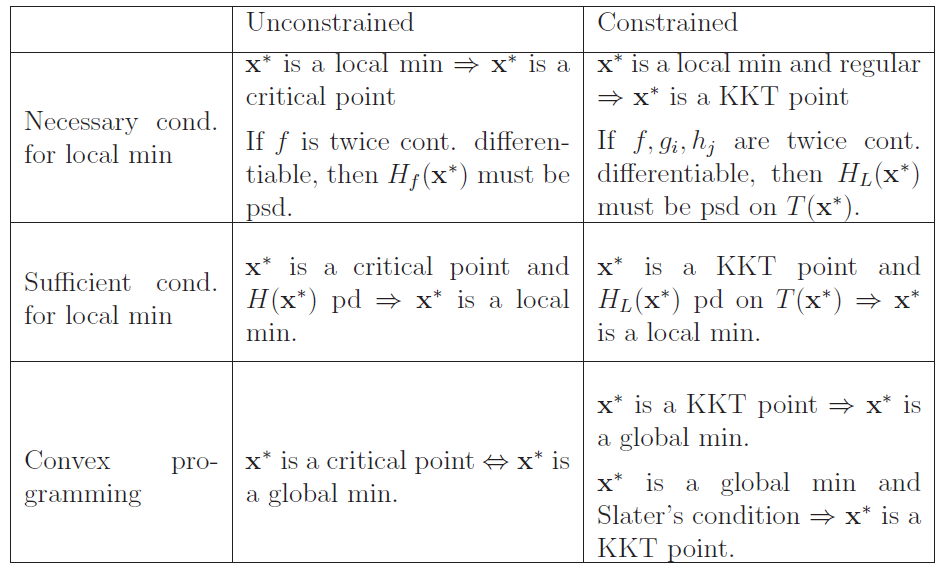
3. Constrained Convex Optimization
3.1.1 Alternating Projection
find intersection of two sets.
alternating projection:
$$
\begin{array}{l}{x^{k+1}:=\Pi_{\mathcal{C}}\left(z^{k}\right)} \ {z^{k+1}:=\Pi_{\mathcal{D}}\left(x^{k+1}\right)}\end{array}
$$
ADMM:
$$
\begin{array}{ll}
\min & f(x)+g(z) \
\text{s.t. } & x-z = 0
\end{array}
$$
where $f$ and $g$ are indicator function of $\mathcal C$ and $\mathcal D$.
$$
\begin{array}{l}{x^{k+1}:=\Pi_{\mathcal{C}}\left(z^{k}-u^k\right)} \ {z^{k+1}:=\Pi_{\mathcal{D}}\left(x^{k+1}+u^k\right)} \
u^{k+1} := u^k+x^{k+1}-z^{k+1} \end{array}
$$
This ADMM method is more efficient than previous method.
3.1.2 Parallel Projection
find a point in the intersection of $N$ sets $\mathcal A_1, \cdots, \mathcal A_N$.
So, $\mathcal C=\mathcal A_1\times \cdots \times \mathcal A_N$, $\mathcal D={(x_1, \cdots, x_N) \in \mathbb R^{nN} | x_1 = \cdots = x_N }$.
So, $\Pi_\mathcal C(x) = (\Pi_{\mathcal A_1}(x_1), \cdots, \Pi_{\mathcal A_N}(x_N))$, $\Pi_\mathcal D(x)=(\bar x, \cdots, \bar x)$, where $\bar x = \frac{1}{N}\sum_{i=1}^N x_i$.
each step of ADMM can be carried out by projecting points onto each of the sets $\mathcal A_i$ in parallel and then averaging the results:
$$
\begin{aligned} x_{i}^{k+1} &:=\prod_{\mathcal{A}{i}}\left(z^{k}-u{i}^{k}\right) \ z^{k+1} &:=\frac{1}{N} \sum_{i=1}^{N}\left(x_{i}^{k+1}+u_{i}^{k}\right) \ u_{i}^{k+1} &:=u_{i}^{k}+x_{i}^{k+1}-z^{k+1} \end{aligned}
$$
The first and third steps can be carried out in parallel.
indicator function of $\mathcal A_1 \cap \cdots \cap \mathcal A_N$ splits into the sum of the indicator functions of each $\mathcal A_i$.
Another compact representation:
$$
\begin{array}{ll}
&x_i^{k+1} = \Pi_{\mathcal A_i}(\bar x^k - u_i^k) \
&u_i^{k+1} = u_i^k + (x_i^{k+1}-\bar x^{k+1}) \
\text{where} & \bar u^{k+1}=\bar u^k+\bar x^{k+1}- z^k, z^{k+1} = \bar x^{k+1}+\bar u^k
\end{array}
$$
This shows that the $u_i^k$ is the running sum of the discrepancies $x_i^k-\bar x^k$. The first step is a parallel projection onto the sets $\mathcal C_i$; the second involves averaging the projected points.
3.2 Linear and Quadratic Programming
Quadratic program (QP)
$$
\begin{array}{rc}
\min & \frac{1}{2}x^TPx + q^Tx \
\text{s.t. } & Ax=b, x\ge 0
\end{array}
$$
where $x\in \mathbb R^n$, $P\in \mathbb S_+^n$.
Represent it as ADMM form as
$$
\begin{array}{rcc}
&\min & f(x)+g(z) \
&\text{s.t. } & x-z=0 \
\text{where, } & &f(x)=\frac{1}{2}x^TPx + q^Tx, & \mathrm{dom} f={x|Ax=b}, & g(z)=\delta_{\mathbb R_+^n}(z)
\end{array}
$$
$f$ is the original objective with restricted domain and $g$ is the indicator function of $\mathbb R_+^n$.
Scaled form of ADMM:
$$
\begin{aligned}
x^{k+1} &:=\operatorname{argmin}{x}\left(f(x)+\frac{\sigma}{2} \left|x-z^{k}+u^{k}\right|^{2}\right) \
z^{k+1} &:=\left(x^{k+1}+u^{k}\right){+} \
u^{k+1} &:=u^{k}+x^{k+1}-z^{k+1}
\end{aligned}
$$
Here, the $x$-update is an equality-constrained least square problem with optimality KKT conditions, $\nu$ is multiplier.
$$
\begin{bmatrix}{P+\sigma I} & {A^{T}} \ {A} & {0}\end{bmatrix} \begin{bmatrix}{x^{k+1}} \ {\nu}\end{bmatrix} + \begin{bmatrix}{q-\sigma\left(z^{k}-u^{k}\right)} \ {-b}\end{bmatrix} = 0
$$
Linear and Quadratic Cone Programming
conic constraint $x\in \mathcal K$ to replace $x\ge 0$ above
The only change to ADMM is the $z$-update (Projection onto $\mathcal K$)
For example, we can solve a semidefinite program with $x \in \mathbb S^n_+$ by projecting $x^{k+1} + u^k$ onto $\mathbb S^n_+$ using an ==eigenvalue decomposition==.
4. $\ell_1$ Norm Problems
ADMM explicitly targets problems that split into two distinct parts, $f$ and $g$, that can then be handled separately.
ADMM can decouple the nonsmooth $\ell_1$ term from the smooth loss term.
4.1 Least Absolute Deviations
minimize $|Ax-b|_1$ instead of $|Ax-b|_2^2$. provide a more robust fit than least squares
ADMM form:
$$
\begin{array}{ll}
\min & |z|_1 \
\text{s.t. } & Ax-z=b
\end{array}
$$
so, $f=0$, $g=| \cdot|_1$.
ADMM algorithm:
$$
\begin{aligned}
x^{k+1} &:= (A^TA)^{-1} A^T (b+z^k-u^k) \
z^{k+1} &:= S_{\frac{1}{\sigma}}(Ax^{k+1}-b+u^k) \
u^{k+1} &:= u^{k} + Ax^{k+1} - z^{k+1} - b
\end{aligned}
$$
Huber fitting
between least square and lease absolute.
$$
\begin{array}
{} &\min & g^{\text{hub}}(Ax-b) \
\text{where} & &g^{\text{hub}}(a)= \begin{cases} \frac{a^2}{2},\quad & |a|\le 1 \ |a|-\frac{1}{2},\quad & |a|>1 \end{cases} &
\end{array}
$$
ADMM algorithm:
same. Only difference is the $z$-update
$$
z^{k+1}:=\frac{\sigma}{1+\sigma}\left(A x^{k+1}-b+u^{k}\right)+\frac{1}{1+\sigma} S_{1+1 / \sigma}\left(A x^{k+1}-b+u^{k}\right)
$$
4.2 Basis Pursuit
$$
\begin{array}{ll}
\min & |x|_1 \
\text{s.t. } & Ax=b
\end{array}
$$
with $x\in \mathbb R^n$, $A\in \mathbb R^{m\times n}$, $b\in \mathbb R^m$ ($m<n$).
Aim: to find a sparse solution to an underdetermined system with equality equations.
ADMM form:
$$
\begin{array}{ll}
\min & f(x)+|z|_1 \
\text{s.t. } & x-z=0
\end{array}
$$
where $f$ is indicator function of set $\mathcal C={x\in \mathbb R^n | Ax=b}$.
ADMM algorithm:
$$
\begin{aligned}
x^{k+1} &:= \Pi_\mathcal C (z^k-u^k) \
z^{k+1} &:= S_{\frac{1}{\sigma}}(x^{k+1}+u^k) \
u^{k+1} &:= u^{k} + x^{k+1} - z^{k+1}
\end{aligned}
$$
The subproblem of $x$-update is solving a linearly-constrained minimum Euclidean norm problem
$$
x^{k+1} = (I-A^T (AA^T)^{-1} A)(z^k-u^k) + A^T(AA^T)^{-1}b
$$
4.3 General $\ell_1$ regularized loss minimization
Problem: $\min \quad l(x)+\lambda |x|_1$
ADMM form:
$$
\begin{array}{rll}
&\min & l(x)+g(z) \
&\text{s.t. } & x-z=0 \
\text{where,} & & g(z)=\lambda |z|1
\end{array}
$$
ADMM algorithm:
$$
\begin{aligned}
x^{k+1} &:=\operatorname{argmin}{x}\left(l(x)+\frac{\sigma}{2} \left|x-z^{k}+u^{k}\right|^{2}\right) \
z^{k+1} &:= S_{\frac{\lambda}{\sigma}}(x^{k+1}+u^k) \
u^{k+1} &:=u^{k}+x^{k+1}-z^{k+1}
\end{aligned}
$$
For subproblem $x$-update:
- If $l$ is smooth, this can be done by any standard method, such as Newton’s method, a quasi-Newton method such as L-BFGS, or the conjugate gradient method.
- If $l$ is quadratic, the $x$-minimization can be carried out by solving linear equations
4.2 Lasso
$$
\min \frac{1}{2} |Ax-b|^2 + \lambda |x|_1
$$
ADMM form:
$$
\begin{array}{rll}
&\min & f(x)+g(z) \
&\text{s.t. } & x-z=0 \
\text{where,} & & f(x)=\frac{1}{2}|Ax-b|^2,\quad g(z)=\lambda |z|1
\end{array}
$$
ADMM algorithm:
$$
\begin{aligned}
x^{k+1} &:= (A^TA+\sigma I)^{-1} (A^Tb+\sigma(z^k-u^k)) \
z^{k+1} &:= S{\frac{\lambda}{\sigma}}(Ax^{k+1}-b+u^k) \
u^{k+1} &:= u^{k} + Ax^{k+1} - z^{k+1}
\end{aligned}
$$
4.4.1 Generalized Lass
$$
\min \frac{1}{2} |Ax-b|^2 + \lambda |Fx|_1
$$
where $F$ is an arbitrary linear transformation.
==Special cases:==
$$
F_{ij}=\begin{cases} 1, \quad & j=i+1 \ -1, \quad & j=i \ 0, \quad & \text{otherwise} \end{cases}
$$
and $A=I$, the generation reduces to
$$
\min \frac{1}{2} |x-b|^2 + \lambda \sum_{i=1}^{n-1} |x_{i+1}-x_i|
$$
ADMM form:
$$
\begin{array}{rll}
&\min & \frac{1}{2} |Ax-b|^2 + \lambda |z|1\
&\text{s.t. } & Fx-z=0 \
\end{array}
$$
ADMM algorithm:
$$
\begin{aligned}
x^{k+1} &:= (A^TA+\sigma F^TF)^{-1} (A^Tb+\sigma F^T(z^k-u^k)) \
z^{k+1} &:= S{\frac{\lambda}{\sigma}}(Fx^{k+1}+u^k) \
u^{k+1} &:= u^{k} + Fx^{k+1} - z^{k+1}
\end{aligned}
$$
For the previous special case, the $A^TA+\sigma F^TF$ is tridiagonal, so can be carried out in $O(n)$ flops.
4.4.2 Group Lasso
Replace $|x|1$ with $\sum{i=1}^N |x_i|_2$ where $x=(x_1, \cdots, x_N)$ with $x_i \in \mathbb R^{n_i}$.
All the same, except the $z$-update:
$$
z_i^{k+1} := S_{\frac{\lambda}{\sigma}}(x_i^{k+1}+u^k), \quad o=1, \cdots, N \
$$
where the thresholding operator $S_\kappa$ is
$$
S_\kappa(a)=(1-\frac{\kappa}{|a|2} )+ a
$$
Extend to handle the overlapping groups.
$N$ potentially overlapping groups $G_i \subseteq {1,\cdots, n}$, the objective is
$$
\frac{1}{2} |Ax-b|^2 + \lambda \sum_{i=1}^N |x_{G_i} |
$$
because the groups can overlap, this kind of objective is difficult to optimize with many standard methods, but it is straightforward with ADMM.
ADMM: Introduce $x_i\in \mathbb R^{|G_i|}$ and consider problem:
$$
\begin{array}{ll}
\min & \frac{1}{2} |Az-b|^2 + \lambda \sum_{i=1}^N |x_i| \
\text{s.t. } & x_i-\tilde z_i=0, i=1, \cdots, N
\end{array}
$$
Sparse Inverse Covariance Selection
5. Consensus and Sharing
$$
\min f(x) = \sum_{i=1}^N f_i(x)
$$
5.1 Global Variable Consensus
Global consensus problem:
add global consensus variable $z$ to split the minimization problem
$$
\begin{aligned}
\min \quad& \sum_{i=1}^N f_i(x_i) \
\text{s.t.} \quad& x_i-z = 0, \ i=1,\cdots,N
\end{aligned}
$$
constraint means all the local variables $x_i$ should be equal.
Augmented Lagrangian:
$$
L_\sigma(x_1, \cdots, x_N, z, y) = \sum_{i=1}^N \left( f_i(x_i) + y_i^T(x_i-z) + \frac{\sigma}{2} |x_i-z|^2 \right)
$$
constraint set is
$$
\mathcal C = {(x_1, \cdots, x_N) | x_1=x_2=\cdots=x_N }
$$
ADMM algorithm:
$$
\begin{aligned}
x_i^{k+1} &:= \mathop{\mathrm{argmin}}{x_i} \left( f_i(x_i)+y_i^{kT}(x_i-z^k)+\frac{\sigma}{2}|x_i-z^k|^2 \right) \
z^{k+1} &:= \frac{1}{N} \sum{i=1}^N \left( x_i^{k+1} + \frac{1}{\sigma}y_i^k \right) \
y_i^{k+1} &:= y^k_i + \sigma(x_i^{k+1}-z^{k+1})
\end{aligned}
$$
Here, the first and last step can be carried out independently.
Simplify this algorithm:
$$
\begin{array}{ll}
&\begin{aligned}
x_i^{k+1} &:= \mathop{\mathrm{argmin}}_{x_i} \left( f_i(x_i)+y_i^{kT}(x_i-z^k)+\frac{\sigma}{2}|x_i-\bar x^k|^2 \right) \
y_i^{k+1} &:= y^k_i + \sigma(x_i^{k+1}-\bar x^{k+1})
\end{aligned} \
\text{where, } & \quad z^{k+1} = \bar x^{k+1} + \frac{1}{\sigma} \bar y^k \
\end{array}
$$
The dual variables are separately updated to drive the variables into consensus, and quadratic regularization helps pull the variables toward their average value while still attempting to minimize each local $f_i$.
We can interpret consensus ADMM as a method for solving problems in which the objective and constraints are distributed across multiple processors. Each processor only has to handle its own objective and constraint term, plus a quadratic term which is updated each iteration. The quadratic terms (or more accurately, the linear parts of the quadratic terms) are updated in such a way that the variables converge to a common value, which is the solution of the full problem.
Primal and dual residual are
$$
{r^{k}=\left(x_{1}^{k}-\bar{x}^{k}, \ldots, x_{N}^{k}-\bar{x}^{k}\right), \quad s^{k}=-\sigma\left(\bar{x}^{k}-\bar{x}^{k-1}, \ldots, \bar{x}^{k}-\bar{x}^{k-1}\right)}
$$
So, the square norms are
$$
{\qquad\left|r^{k}\right|{2}^{2}=\sum{i=1}^{N}\left|x_{i}^{k}-\bar{x}^{k}\right|{2}^{2}, \quad\left|s^{k}\right|{2}^{2}=N \sigma^{2}\left|\bar{x}^{k}-\bar{x}^{k-1}\right|_{2}^{2}}
$$
5.1.2 Global Variable Consensus with Regularization
$$
\begin{array}{ll}
\min & \sum_{i=1}^N f_i(x_i) + g(z) \
\text{s.t. } & x_i-z=0, i=1,\cdots, N
\end{array}
$$
ADMM algorithm:
$$
\begin{array}{l}{x_{i}^{k+1}:=\underset{x_{i}}{\operatorname{argmin}}\left(f_{i}\left(x_{i}\right)+y_{i}^{k T}\left(x_{i}-z^{k}\right)+\frac{\sigma}{2} \left|x_{i}-z^{k}\right|{2}^{2}\right)} \ {z^{k+1}:=\underset{z}{\operatorname{argmin}}\left(g(z)+\sum{i=1}^{N}\left(-y_{i}^{k T} z+\frac{\sigma}{2} \left|x_{i}^{k+1}-z\right|{2}^{2}\right)\right)} \ {y{i}^{k+1}:=y_{i}^{k}+\sigma\left(x_{i}^{k+1}-z^{k+1}\right)} \end{array}
$$
Express the $z$-update as an averaging step, so we can have
$$
{\quad z^{k+1}:=\underset{z}{\operatorname{argmin}}\left(g(z)+\frac{N\sigma}{2}\left|z-\bar{x}^{k+1}-\frac{1}{\sigma} \bar{y}^{k}\right|_{2}^{2}\right)}
$$
example 1:
$g(z)=\lambda |z|1$, $z$-update becomes $z^{k+1}:=S{\frac{\lambda}{N\sigma}}(\bar x^{k+1}-\frac{1}{\sigma} \bar y^k)$
Example 2:
$g$ is indicator function of $\mathbb R^n_+$, i.e., $g=\delta_{\mathbb R_+^n}$. $z$-update is $z^{k+1}:=(\bar x^{k+1}-\frac{1}{\sigma} \bar y^k)_+$
Algorithm:
$$
\begin{array}{l}{x_{i}^{k+1}:=\underset{x_{i}}{\operatorname{argmin}}\left(f_{i}\left(x_{i}\right)+\frac{\sigma}{2} \left|x_{i}-z^{k}+u_i^k\right|{2}^{2}\right)} \
{z^{k+1}:=\underset{z}{\operatorname{argmin}}\left(g(z)+\frac{N\sigma}{2} \left|z-x{i}^{k+1}-\bar u^k\right|{2}^{2}\right)} \
{u{i}^{k+1}:=u_{i}^{k}+x_{i}^{k+1}-z^{k+1}} \end{array}
$$
Objective: $f_1(x_1) + \cdots + f_N(x_N)$. Each of these local variables consists of a selection of the components of the global variables $z\in \mathbb R^n$. This means each components of local variable corresponds to some global variable component $z_g$.
Mapping from local to global: $g=\mathcal G(i,j)$
In the context of model fitting, the following is one way that general form consensus naturally arises. The global variable $z$ is the full feature vector (i.e., vector of model parameters or independent variables in the data), and different subsets of the data are spread out among $N$ processors. Then xi can be viewed as the subvector of $z$ corresponding to (nonzero) features that appear in the $i$th block of data. In other words, each processor handles only its block of data and only the subset of model coefficients that are relevant for that block of data. If in each block of data all regressors appear with nonzero values, then this reduces to global consensus.
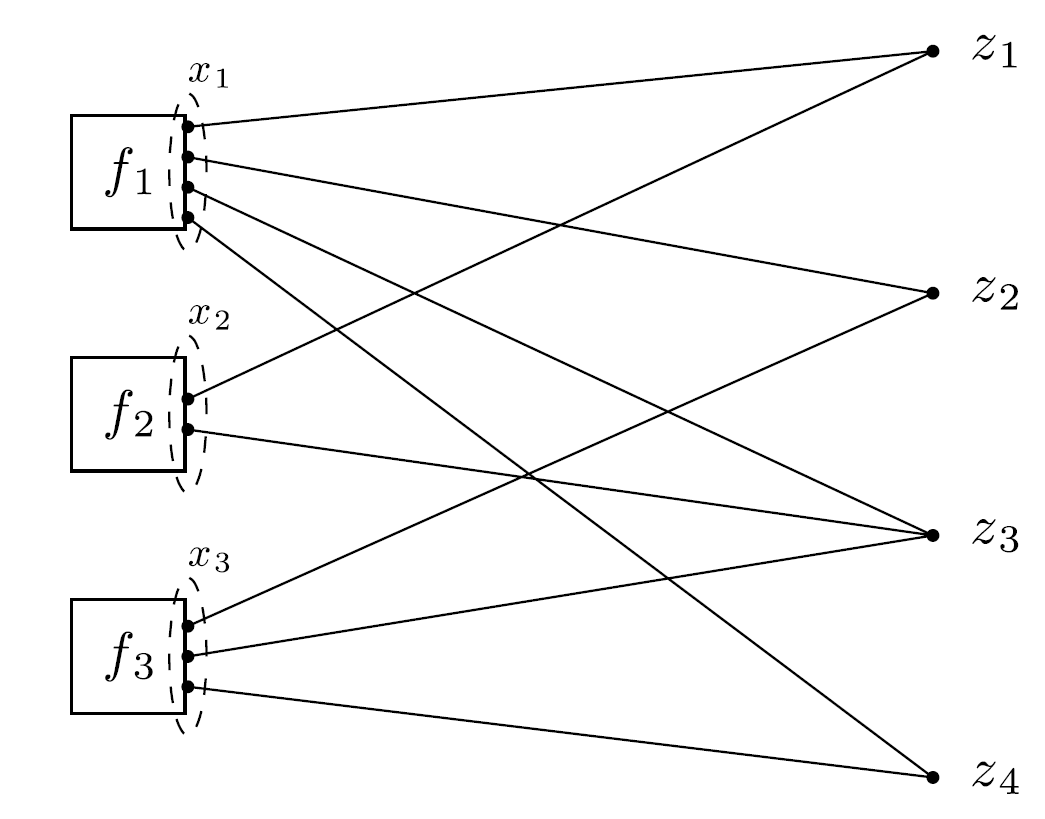
$\tilde z_i \in \mathbb R^{n_i}$ defined by $(\tilde z_i)j = z{\mathcal G(i,j)}$.
General form consensus problem is
$$
\begin{array}{ll}
\min & \sum_{i=1}^N f_i(x_i) \
\text{s.t. }& x_i-\tilde z_i = 0, i = 1, \cdots, N
\end{array}
$$
Augmented Lagrangian is
$$
L_\sigma(x,z,y) = \sum_{i=1}^N \left( f_i(x_i) + y^T_i(x_i-\tilde z_i) + \frac{
\sigma}{2} |x_i - \tilde z_i |^2 \right)
$$
with the dual variables $y_i\in \mathbb R^{n_i}$.
ADMM algorithm:
$$
\begin{array}{l}
{x_{i}^{k+1}:=\underset{x_{i}}{\operatorname{argmin}}\left(f_{i}\left(x_{i}\right)+y_{i}^{k T}x_{i}+\frac{\sigma}{2} \left|x_{i}-\tilde z_i^{k}\right|{2}^{2}\right)} \ {z^{k+1}:=\underset{z}{\operatorname{argmin}}\left(\sum{i=1}^{m}\left(-y_{i}^{k T} \tilde z_i+\frac{\sigma}{2} \left|x_{i}^{k+1}-\tilde z_i\right|{2}^{2}\right)\right)} \ {y{i}^{k+1}:=y_{i}^{k}+\sigma\left(x_{i}^{k+1}-\tilde z_i^{k+1}\right)}
\end{array}
$$
where $x_i$- and $y_i$- updates can be carried out independently for each $i$.
The $z$- update step decouples across the components of $z$, since $L_\sigma$ is fully separable in its components:
$$
z_{g}^{k+1}:=\frac{\sum_{\mathcal{G}(i, j)=g}\left(\left(x_{i}^{k+1}\right){j}+(1 / \sigma)\left(y{i}^{k}\right){j}\right)}{\sum{\mathcal{G}(i, j)=g} 1}
$$
the $z$-update is local averaging for each component $z_g$ rather than global averaging;
in the language of collaborative filtering, we could say that only the processing elements that have an opinion on a feature $z_g$ will vote on $z_g$.
$$
\begin{array}{ll}
\min & \sum_{i=1}^N f_i(x_i) + g(z) \
\text{s.t. }& x_i-\tilde z_i = 0, i = 1, \cdots, N
\end{array}
$$
where $g$ is a regularization function.
$z$-update:
- first, the local averaging step from the unregularized setting, same to compute $z_g^{k+1}$.
- Then, proximity operator $\mathrm{Prox}_{g,k_g\sigma}$ for averaging
5.3 Sharing
$$
\min \sum_{i=1}^N f_i(x_i) + g(\sum_{i=1}^N x_i)
$$
where $x_i\in \mathbb R^n, i=1,\cdots, N$. $g$ is the shared object.
Problem:
$$
\begin{array}{ll}
\min & \sum_{i=1}^N f_i(x_i) + g(\sum_{i=1}^N z_i) \
\text{s.t. }& x_i- z_i = 0, \quad x_i, z_i \in \mathbb R^n, \quad i = 1, \cdots, N, \quad
\end{array}
$$
The scaled ADMM algorithm;
$$
\begin{array}{l}
{x_{i}^{k+1}:=\underset{x_{i}}{\operatorname{argmin}}\left(f_{i}\left(x_{i}\right)+\frac{\sigma}{2} \left|x_{i}- z_i^{k}+u_i^k\right|{2}^{2}\right)} \
{z^{k+1}:=\underset{z}{\operatorname{argmin}}\left(g\left(\sum{i=1}^{N}z_i\right) + \frac{\sigma}{2} \sum_{i=1}^N \left|z_i-x_{i}^{k+1}-u_i^k\right|{2}^{2}\right)} \ {u{i}^{k+1}:=u_{i}^{k}+x_{i}^{k+1}- z_i^{k+1}}
\end{array}
$$
$x_i$- and $u_i$ update can be carried out independently. $z$-update solve problem in $Nn$ variables.
But we can simplify it to solve only $n$ variables.
$$
\begin{array}{ll}
&\min & g(N\bar z)+\frac{\sigma}{2} \sum_{i=1}^N |z+i-a_i|^2 \
&\text{s.t. } & \bar z=\frac{1}{N} \sum_{i=1}^N z_i \
\text{where,} && a_i = u_i+x_i^{k+1}
\end{array}
$$
Because $\bar z$ fixed, we have $z_i = a_i +\bar z+\bar a$.
So, $z$-update can be computed by solving unconstrained problem
$$
\min \quad g(N\bar z)+\frac{\sigma}{2} \sum_{i=1}^N |\bar z - \bar a |^2
$$
Then, we can have
$$
u_i^{k+1} = \bar u^k + \bar x^{k+1} - \bar z^{k+1}
$$
It’s obvious that all of the dual variables $u_i^k$ are equal, (i.e., consensus), and can be replaces with a single dual variable $u\in \mathbb R^m$.
So, the final algorithm:
$$
\begin{array}{l}
{x_{i}^{k+1}:=\underset{x_{i}}{\operatorname{argmin}}\left(f_{i}\left(x_{i}\right)+\frac{\sigma}{2} \left|x_{i}-x_i^k+\bar x^k - \bar z^{k}+u^k\right|{2}^{2}\right)} \
{\bar z^{k+1}:=\underset{\bar z}{\operatorname{argmin}}\left(g\left(N \bar z\right) + \frac{N\sigma}{2} \left|\bar z-u^k-\bar x^{k+1}\right|{2}^{2}\right)} \ {u^{k+1}:=u^{k}+\bar x^{k+1}- \bar z^{k+1}}
\end{array}
$$
The $x$-update can be carried out in parallel, for $i = 1,\cdots,N$. The $z$-update step requires gathering $x^{k+1}_i$ to form the averages, and then solving a problem with $n$ variables. After the $u$-update, the new value of $\bar x^{k+1} − \bar z^{k+1} + u^{k+1}$ is scattered to the subsystems.
5.3.1 Duality
Attaching Lagrange multipliers $\nu_i$ to the constraints $x_i-z_i=0$, the dual function $\Gamma$ of the ADMM sharing problem is
$$
\Gamma(\nu_1, \cdots, \nu_N) = \begin{cases} -g^*(\nu_1)-\sum_if^*i(-\nu_i), \quad &\text{if }\nu_1=\nu_2=\cdots=\nu_N \ -\infty, \quad &\text{otherwise} \end{cases}
$$
Letting $\psi=g^*$, $h_i(\nu)=f^*(-\nu)$, the dual problem can be rewritten as
$$
\begin{array}{ll}
\min & \sum{i=1}^N h_i(\nu_i) +\psi(\nu) \
\text{s.t. } & \nu_i-\nu=0
\end{array}
$$
This is same as the regularized global variable consensus problem.
$d_i\in \mathbb R^n$ is the multiplers to constraints $\nu_i-\nu=0$. So, the Dual regularized global consensus problem is
$$
\min \quad \sum_{i=1}^N f_i(d_i) + g(\sum_{i=1}^N d_i)
$$
Thus, there is a close dual relationship between the consensus problem and the sharing problem. In fact, the global consensus problem can be solved by running ADMM on its dual sharing problem, and vice versa.
5.3.2 Optimal Exchange
exchange problem:
$$
\begin{array}{ll}
\min & \sum_{i=1}^N f_i(x_i) \
\text{s.t.} & \sum_{i=1}^N x_i=0
\end{array}
$$
The sharing objective $g$ is the indicator function of the set ${0}$. The components of the vectors $x_i$ represent quantities of commodities that are exchanged among $N$ agents or subsystems. $(x_i)_j$ is the exchanging amount. If $(x_i)_j>0$, $i$ send to $j$, and vice versa. Constraints $\sum x_i=0$ means the each commodity clears.
Scaled ADMM algorithm:
$$
\begin{aligned}
x_i^{k+1} &= \mathop{\operatorname{argmin}}{x_i} \left( f_i(x_i) + \frac{\sigma}{2} |x_i-x_i^k+\bar x^k+u^k |^2 \right) \
u^{k+1} &= u^k + \bar x^{k+1}
\end{aligned}
$$
Unscaled ADMM algorithm:
$$
\begin{aligned}
x_i^{k+1} &= \mathop{\operatorname{argmin}}{x_i} \left( f_i(x_i) + y^{kT}x_i + \frac{\sigma}{2} |x_i-(x_i^k-\bar x^k) |^2 \right) \
y^{k+1} &= y^k + \sigma \bar x^{k+1}
\end{aligned}
$$
The proximal term in the $x$-update is a penalty for $x^{k+1}$ deviating from $x^k$, projected onto the feasible set.
$x$-update can be carried out in parallel. $u$-update needs gathering $x_i^{k+1}$ and averages it, then broadcast $u^k + \bar x^{k+1}$ back for $x$-update
Dual decomposition is the simplest algorithmic expression of this kind of problem. In this setting, each agent adjusts his consumption $x_i$ to minimize his individual cost $f_i(x_i)$ adjusted by the cost $y^T x_i$, where $y$ is the price vector. ADMM differs only in the inclusion of the proximal regularization term in the updates for each agent. As $y^k$ converges to an optimal price vector $y^*$, the effect of the proximal regularization term vanishes. The proximal regularization term can be interpreted as each agent’s commitment to help clear the market.
6. Distributed Model Fitting
$$
\min l(Ax-b) + r(x)
$$
where $l(Ax-b)=\sum_{i=1}^m l_i(a_i^Tx-b_i)$.
assume the regularization function $r$ is separable, like $r(x)=\lambda |x|_2^2$ or $r(x)=\lambda |x|_1$
7. Nonconvex
7.1 Nonconvex constraints
$$
\begin{array}{ll}
\min & f(x) \
\text{s.t.} & x\in \mathbb S
\end{array}
$$
with $f$ convex but $\mathbb S$.
$$
\begin{array}{l}{x^{k+1}:=\underset{x}{\operatorname{argmin}}\left(f(x)+(\rho / 2)\left|x-z^{k}+u^{k}\right|{2}^{2}\right)} \ {z^{k+1}:=\prod{\mathcal{S}}\left(x^{k+1}+u^{k}\right)} \ {u^{k+1}:=u^{k}+x^{k+1}-z^{k+1}}\end{array}
$$
Here, $x$-minimization step is convex since $f$ is convex, but $z$-update is projection onto nonconvex set.
- Cardinality. If $\mathbb S = {x | \mathrm {card}(x) ≤ c}$, where $\mathrm{card}$ gives the number of nonzero elements, then $\Pi_{\mathbb S}(v)$ keeps the $c$ largest
magnitude elements and zeroes out the rest.
- Rank. If $\mathbb S$ is the set of matrices with rank $c$, then $\Pi_{\mathbb S}(v)$ is determined by carrying out a singular value decomposition, $v =\sum_i \sigma_i u_i v_i^T$, and keeping the top $c$ dyads, i.e., form $\Pi_{\mathbb S}(v) = \sum_{i=1}^c \sigma_i u_i v_i^T$.
- Boolean constraints. If $\mathbb S={ x|x_i\in {0,1} }$, then $\Pi_{\mathbb S}(v)$ simply rounds each entry to 0 or 1, whichever is closer. Integer constraints can be handled in the same way.
8. QCQP
$$
\begin{array}{rCl}
\text{(P1)} &
\begin{array}{rCl}
&\min\limits_{x \in \mathbb{R}^{n}} & x^{T} C x\
&\text { s.t. } &x^{T} A_{i} x \underline\triangleright b_{i}, \quad i=1, \dots, m
\end{array}
\end{array}
$$
where $\underline\triangleright$ can represents either $\geq, \leq, =$; $C, A_1, A_2, \cdots, A_m \in \mathbb S^n$ where $\mathbb S^n$ denotes the set of all real symmetric $n\times n$ matrices.
if $A_i$ are positive semidefinite, it’s convex program. many nonlinear programming codes can be used. (primal-dual interior-point method)
Nonconvex QOP is NP-hard. there are two distinct techniques –> branch-and-bound method
generate a feasible solution or approximate feasible solution with a smaller objective value.
derive a tighter lower bound of the minimal objective value
“Lift-and-project convex relaxation methods” can be characterized as three steps:
Lift the QOP to an equivalent problem in the space $\mathbb S^{1+n}$ of $(1+n)\times(1+n)$ symmetric matrices. The resulting problem is an Linear Programming with additional rank-1 and positive semidefinite constraints imposed on a matrix variable
$$
Y=\begin{pmatrix} 1 & x^T \ x & X \end{pmatrix} \in \mathbb S^{1+n}
$$
Relax the rank-1 and positive semidefinite constraints so that the feasible region of the resulting problem is convex.
Project the relaxed lifted problem in $\mathbb S^{1+n}$ back to the original Euclidean space $\mathbb R^n$.
If only the rank-1 constraint is removed in step 2, it becomes an SDP –> SDP relaxation
If remove both rank-1 and positive semidefinite constraints in step 2, it becomes LP. –> cutting plane algorithm, LP relaxation
The SDP relaxation is at least as effective as LP relaxation. More efficient. 0.878 approximation of maximum cut based on the SDP relaxation is widely known.
8.1 SDR
8.1.1 Homogeneous QCQP
$$
\begin{array}{rCCCl}
x^{T} C x &=& \operatorname{Tr}\left(x^{T} C x\right) & = & \operatorname{Tr}\left(C x x^{T}\right) \
x^{T} A_{i} x &=& \operatorname{Tr}\left(x^{T} A_{i} x\right) & = & \operatorname{Tr}\left(A_{i} x x^{T}\right)
\end{array}
$$
Set $xx^T = X$.
Equivalent formulation is
$$
\begin{array}{rCl}
\text{(P2)} &
\begin{array}{rCl}
&\min\limits_{X \in \mathbb{S}^{n}} & \operatorname{Tr}(C X)\
&\text { s.t. } & \operatorname{Tr}(A_{i} X) \underline\triangleright b_{i}, \quad i=1, \dots, m \
&& X\succeq 0, : \operatorname{rank}(X) = 1
\end{array}
\end{array}
$$
In problem (P2), the rank constraint $\operatorname{rank}(X)=1$ is difficult and nonconvex. Thus, it can be dropped to obtain the relaxed version (P3):
$$
\begin{array}{rCl}
\text{(P3)} &
\begin{array}{rCl}
&\min\limits_{X \in \mathbb{S}^{n}} & \operatorname{Tr}(C X)\
&\text { s.t. } & \operatorname{Tr}(A_{i} X) \underline\triangleright b_{i}, \quad i=1, \dots, m \
&& X\succeq 0
\end{array}
\end{array}
$$
Most of the convex optimization toolboxes handles SDPs using interior-point algorithm with the worst complexity $\mathcal O(\max{m,n}^4n^{1/2}\log(1/\epsilon))$ given a solution accuracy $\epsilon>0$. [Primal-dual path-following method]
SDR is a computationally efficient approximation approach to QCQP, in the sense that its complexity is polynomial in the problem size $n$ and the number of constraints $m$.
But, how to convert a globally optimal solution $X^*$ to a feasible solution $\tilde x$ is hard if $\operatorname{rank}(X) \neq 1$. Even if we obtain $\tilde x$, it may be not optimal solution $x^*$.
one method:
- If $\operatorname{rank}(X) \neq 1$, let $r=\operatorname{rank}(X^*)$, let $X^* = \sum_{i=1}^r \lambda_i q_iq_i^T$ denote the eigen-decomposition of $X^*$ where $\lambda_1\ge \lambda_2 \ge \cdots \ge \lambda_r \ge 0$ are eigen values ad $q_1, q_2, \cdots, q_r\in \mathbb R^n$ are eigen vectors. use the best rank-one approximation $X_1^*$ to $X^*$, where $X_1^* = \lambda_1q_1q_1^T$, we have $\tilde x = \sqrt{\lambda_1}q_1$ is one of the solution to (P1)
- Randomization. rounding to generate feasible points from the random samples $\xi_l$. Moreover, we repeat the random sampling $L$ times and choose the one that yields the best objective.
8.1.2 Inhomogeneous QCQP
$$
\begin{array}{rCl}
\min\limits_{x \in \mathbb{R}^{n}} & x^{T} C x+2 c^{T} x \
\text { s.t. } & x^{T} A_{i} x+2 a_{i}^{T} x \underline\triangleright b_{i}, \quad i=1, \ldots, m
\end{array}
$$
rewrite it as homogeneous form
$$
\begin{array}{rCl}
\min\limits_{x \in \mathbb{R}^{n}, t \in \mathbb{R}} & \begin{bmatrix} x^{T} \quad t\end{bmatrix} \begin{bmatrix} C & c \ c^{T} & 0 \end{bmatrix} \begin{bmatrix} x \ t \end{bmatrix} \
\text { s.t. } & t^{2}=1 \
& \begin{bmatrix} x^{T} \quad t\end{bmatrix} \begin{bmatrix} A_i & a_i \ a_i^T & 0 \end{bmatrix} \begin{bmatrix} x \ t \end{bmatrix} \underline\triangleright b_i, \quad i=1, \ldots, m
\end{array}
$$
where both the problem size and the number of constraints increase by one.
8.1.3 Complex-valued problems
One type:
$$
\begin{array}{rCl}
\min\limits_{x \in \mathbb{C}^{n}} & x^{H} C x \
\text { s.t. } & x^{H} A_{i} x : \underline\triangleright : b_{i}, \quad i=1, \ldots, m
\end{array}
$$
where $C, A_1, A_2, \cdots, A_m \in \mathbb H^n$ with $\mathbb H^n$ being the set of all complex $n\times n$ Hermitian matrices.
Convert it as
$$
\begin{array}{rCl}
\min\limits_{X \in \mathbb{H}^{n}} & \operatorname{Tr}(C X)\
\text { s.t. } & \operatorname{Tr}\left(A_{i} X\right) : \underline\triangleright : b_{i}, \quad i=1, \ldots, m\
& X \succeq 0
\end{array}
$$
Another type:
$$
\begin{array}{rCl}
\min\limits_{x \in \mathbb{C}^{n}} &x^{H} C x \
\text { s.t. } &x_{i} \in\left{1, e^{j 2 \pi / k}, \cdots, e^{j 2 \pi(k-1) / k}\right}, i=1, \ldots, n
\end{array}
$$
transform it as
$$
\begin{array}{rCl}
\underset{X \in \mathbb H^{n}}{\min } & \operatorname{Tr}(C X)\
\text { s.t. }& X \succeq 0, : X_{i i}=1, i=1, \ldots, n
\end{array}
$$
8.1.4 Separable QCQPs
$$
\begin{array}{rCl}
\min\limits_{x_{1}, \cdots, x_{k} \in \mathbb{C}^{n}} & \sum\limits_{i=1}^{k} x_{i}^{H} C_{i} x_{i}\
\text { S.t. } & \sum\limits_{l=1}^{k} x_{l}^{H} A_{i, l} x_{l} : \underline\triangleright : b_{i}, \quad i=1, \cdots, m
\end{array}
$$
Let $X_i = x_i x_i^H$ for $i=1,2,\cdots, k$. By relaxing the rank constraint on each $X_i$, we have
$$
\begin{array}{rCl}
\min\limits_{X_{1}, \ldots, X_{k} \in \mathbb{H}^{n}} & \sum\limits_{i=1}^{k} \operatorname{Tr}\left(C_{i} X_{i}\right)\
\text{s.t.} & \sum\limits_{l=1}^{k} \operatorname{Tr}\left(A_{i, l} X_{l}\right) : \underline\triangleright : b_{i}, \quad i=1, \ldots, m\
& X_{1} \succeq 0, \cdots, X_{k} \succeq 0
\end{array}
$$
8.1.5 Application: sensor network
goal: determine the coordinates of sensors in $\mathbb R^2$ such that the distances match the measured distance
Set of sensors $V_s = {1,2, \cdots, n}$, set of anchors $V_a = {n+1, n+2, \cdots, n+m}$.
Let $E_{ss}$ be the sensor-sensor edges, $E_{sa}$ be the set of sensor-anchor edges.
Assume the measured distance ${d_{ik}:(i,k)\in E_{ss}}$ and ${\overline d_{ik}:(i,k) \in E_{sa}}$ are noise-free.
Problem becomes
$$
\begin{array}{rCl}
\text{find} & x_1,x_2,\cdots,x_n \in \mathbb R^2 \
\text{s.t. } & |x_i-x_k|^2 = d_{ik}^2, : (i,k)\in E_{ss} \
& |a_i-x_k|^2 = d_{ik}^2, : (i,k)\in E_{ss} \
\end{array}
$$
First,
$$
|x_i - x_k|^2 = x_i^Tx_i - 2x_i^Tx_k + x_k^Tx_k
$$
rewrite it as
$$
|x_i - x_k|^2 = (e_i-e_k)^TX^TX(e_i-e_k) = \operatorname{Tr}(E_{ik}X^TX)
$$
where $e_i\in \mathbb R^n$ is the $i$th vector, $E_{ik}=(e_i-e_k)^T(e_i-e_k) \in \mathbb S^n$, $X\in \mathbb R^{2\times n}$ whose $i$th column is $x_i$.
Now, we have
$$
|a_i-x_k|^2 = a_i^Ta_i - 2a_i^Tx_k + x_k^Tx_k
$$
Although $a_i^Tx_k$ is linear only in $x_k$, we homogenize it and write as
$$
|a_i-x_k|^2 = \begin{bmatrix} a_i^T & e_k^T \end{bmatrix}\begin{bmatrix} I_2 & X \ x^T & X^TX \end{bmatrix} \begin{bmatrix} a_i \ e_k \end{bmatrix} = \operatorname{Tr}(\bar M_{ik}Z)
$$
where $\bar M_{ik} = \begin{bmatrix} a_i \ e_k \end{bmatrix} \begin{bmatrix} a_i^T & e_k^T \end{bmatrix}\in \mathbb S^{n+2} $ .
Using Schur complement, we have $Z = \begin{bmatrix} I_2 & X \ X^T & X^TX \end{bmatrix} = \begin{bmatrix} I_2 \ X^T \end{bmatrix}\begin{bmatrix} I_2 & X \end{bmatrix} \in \mathbb S^{n+2}$.
Set $M_{ik}= \begin{bmatrix} 0 & 0 \ 0 & E_{ik} \end{bmatrix}$.
We have the following equivalent SDP
$$
\begin{array}{rCl}
\text{find} & Z \
s.t. & \operatorname{Tr}\left(M_{i k} Z\right)=d_{i k}^{2}, \quad(i, k) \in E_{s s} \
& \operatorname{Tr}\left(\bar{M}{i k} Z\right) =\bar{d}{i k}^{2}, \quad(i, k) \in E_{s a} \
& Z_{1: 2,1: 2} =I_{2} \
& Z \succeq 0, : \operatorname{rank}(Z)=2
\end{array}
$$
8.2 Second order cone relaxation (SOCR)
Optimal inverter var control in distribution systems with high pv penetration
Branch flow model: relaxations and convexification (parts I, II)
Optimal power flow in distribution networks
Convex Relaxation of Optimal Power FlowPart I: Formulations and Equivalence
Convex Relaxation of Optimal Power FlowPart II: Exactness,
8.3 Other
SDR/SOCR are not exact.