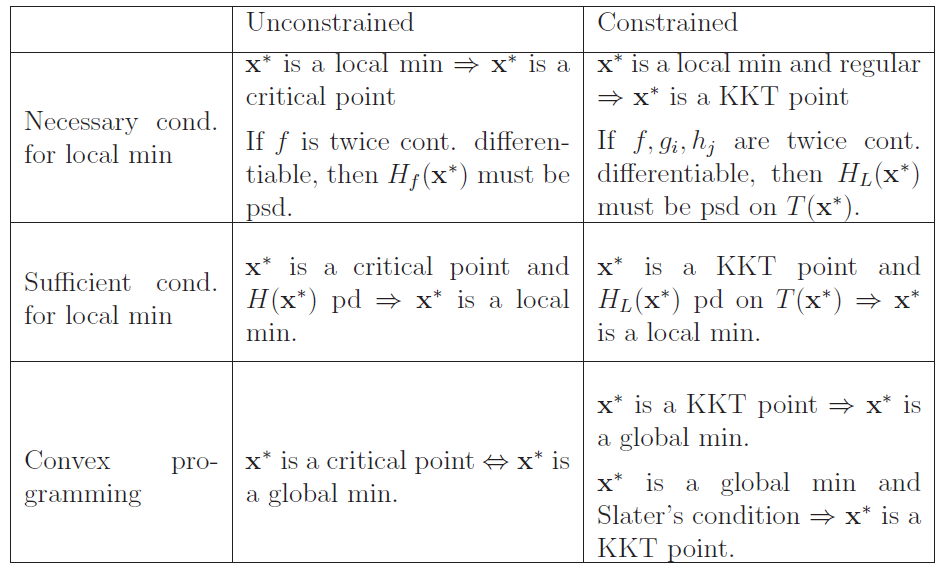
5. Basic Nonlinear Programming

Karush-Kuhn-Tucker (KKT) necessary conditions for local minimizers that generalize the Lagrange Multiplier Method. The KKT necessary conditions are useful in locating possible candidates for a global minimizer.

Constraint qualification

• Active constraints

• Regular point :

  $x^*$ be feasible point of NLP, Let $J(x^*) = \left{ j\in {1, \cdots, p} : h_j(x^*)=0 \right}$ be index set of active constraints at $x^*$. The set of gradient vectors
  $$
  { \nabla g_i(x^*) : i=1, 2, \cdots, m } \cup {\nabla h_j(x^*) : j\in J(x^*) }
  $$
  is linearly independent. $x^*$ is regular point.

Linearly Independence Constraint Qualification (LICQ)

• check whether linear independence, check whether the matrix of all gradient vector of active constraints is full rank.

5.1 KKT necessary conditions

We state the Karush-Kuhn-Tucker necessary conditions for a local minimizer $x^∗$ at which the regularity condition holds

5.1.1 KKT first order necessary conditions:

$$
\begin{aligned} \nabla f\left(\mathrm{x}^{}\right)+\sum_{i=1}^{m} \lambda_{i}^{} \nabla g_{i}\left(\mathrm{x}^{}\right)+\sum_{j=1}^{p} \mu_{j}^{} \nabla h_{j}\left(\mathrm{x}^{}\right) = 0 \ \mu_{j}^{} \geq 0, &\ \forall j=1,2, \cdots, p \ \mu_{j}^{}=0, & \ \forall j \notin J\left(\mathrm{x}^{}\right) \end{aligned}
$$

1. For NLP with no equality constraints, active constraint is only $h_1(x)\leq 0$. So, $\nabla f(x^*) + \mu_1^* \nabla h_1(x^*) = 0$,

   the direction of steep descent $-\nabla f(x^*)$ must be in same direction as $\nabla h_1(x^*)$ onward normal to boundary.

2. For NLP with no equality constraints, only two active constraints, $\nabla f(x^*) + \mu_1^* \nabla h_1(x^*) + \mu_2^* \nabla h_2(x^*) = 0$.

   the direction of steep descent $-\nabla f(x^*)$ must lie in the cone spanned by the outward normals $\nabla h_1(x^*), \nabla h_2(x^*)$ to the boundaries $h_1(x)=0$ and $h_2(x)=0$.

3. For NLP with no equality constraints, $x^*$ is interior of feasible region, $\nabla f(x^*)=0$, as unconstrained minimization problem.

5.1.2 KKT second order necessary condition:

$$
{\qquad H_{L}\left(\mathrm{x}^{}\right) :=H_{f}\left(\mathrm{x}^{}\right)+\sum_{i=1}^{m} \lambda_{i}^{} H_{g_{i}}\left(\mathrm{x}^{}\right)+\sum_{j=1}^{p} \mu_{j}^{} H_{h_{j}}\left(\mathrm{x}^{}\right)}
$$

If $\mathbb x^* $ is a local minimizer, then
$$
{\mathrm{y}^{T} H_{L}\left(\mathrm{x}^{}\right) \mathrm{y} \geq 0}
$$
for all $\mathbb y\in T(\mathbb x^)$, where
$$
T(\mathbb x^*) = \left{ \mathbb y\in \mathbb{R}^n:
\begin{array}{}
\nabla g_{i}\left(\mathrm{x}^{}\right)^{T} \mathbf{y} = 0, i=1,2, \cdots, m \
\nabla h_{j}\left(\mathrm{x}^{}\right)^{T} \mathrm{y} = 0, j \in J\left(\mathrm{x}^{*}\right)
\end{array} \right}
$$

in fact, $T(\mathbb x^*)$ is tangent plane

1. set $T(x^*)$ consists of vectors in the tangent space to $S$ at $x^*$.

   Normal space $N(x^*)$ is subspace spanned by $\nabla g_1(x^*), \cdots, \nabla g_m (x^*), \nabla h_j(x^*), \forall j \in J(x^*)$.

   Tangent space $T(x^*) = { \mathbb y: \mathbb u^T \mathbb y = 0, \forall \mathbb u \in N(\mathbb x^*) }$.

2. For NLP with no equality constraints, if $x^*$ is in interior of feasible region, $T(x^*) = \mathbb R^*$. 2nd KKT becomes $H_L(x^*) = H_f(x^*)$ must be positive semidefinite.

​ easier check for 2nd KKT.

​ matrix $\mathcal D(\mathbb x^*) = \left( \nabla g_1(\mathbb x^*), \cdots, \nabla g_m(\mathbb x^*), [\nabla h_j(\mathbb x^*) : j \in J(\mathbb x^*)] \right)$
$$
\mathbb y^T H_L(\mathbb x^*) \mathbb y \ge 0, \forall \mathbb y \in T(\mathbb x^*) \iff Z(\mathbb x^*)^T H_L(\mathbb x^*) Z(\mathbb x^*) \text{ is positive semidefinite}
$$
​ where $Z(\mathbb x^*)$ is a matrix whose columns forms a basis of the null space of $\mathcal D (\mathbb x^*)$. $T(x) = Z(x) u$

5.1.2 Steps:

1. Check regularity condition
2. verify KKT first order necessary condition.
3. verify KKT second order necessary condition
   1. Hessian matrix
   2. basis of null space of $\mathcal D(\mathbb x^*)^T$
   3. definiteness check

Since the regularity condition for the KKT Theorem is not satisfied, the global minimizer $x^∗$ may not be found among the KKT points.

KKT necessary conditions can be used to find global minimizers.

==Corollary 2.3==

Suppose the following two conditions hold:

1. a global minimizer $x^∗$ is known to exist for an NLP.
2. $x^∗$ is a regular point.

Then $x^∗$ is a KKT point, i.e. there exists $λ^∗ ∈ \mathbb R^m$ and $μ^∗ ∈ \mathbb R^p$ such that the following conditions hold.
$$
\begin{array}{l}{[1] \quad \nabla f\left(\mathrm{x}^{}\right)+\sum_{i=1}^{m} \lambda_{i}^{} \nabla g_{i}\left(\mathrm{x}^{}\right)+\sum_{j=1}^{p} \mu_{j}^{} \nabla h_{j}\left(\mathrm{x}^{}\right)=0} \ {[2] \quad g_{i}\left(\mathrm{x}^{}\right)=0, \quad \forall i=1,2, \cdots, m} \ {[3] \quad \mu_{j}^{} \geq 0, h_{j}\left(\mathrm{x}^{}\right) \leq 0, \quad \mu_{j}^{} h_{j}\left(\mathrm{x}^{}\right)=0, \quad \forall j=1,2, \cdots, p}\end{array}
$$
One approach to use the necessary conditions for solving an NLP is to consider separately all the possible combinations of constraints being active or inactive.

5.2 Interpretation of Lagrange Multipliers

Relax constraints –> relax objective function with the rate of multipliers

5.3 KKT sufficient conditions

the sufficient conditions for a strict local minimizer (or maximizer) do not require regularity conditions.

Let $f, g_i, h_j : \mathbb R^n → \mathbb R, i = 1, 2, · · · ,m$ and $j = 1, 2, · · · , p$, be functions with continuous second partial derivatives. Let $S$ be the feasible set of (NLP). Suppose $\mathbb x^∗ ∈ S$ is a KKT point, i.e., there exist $λ^∗ ∈ \mathbb R^m$ and $μ^∗ ∈ \mathbb R^p$ such that
$$
\nabla f\left(\mathrm{x}^{}\right)+\sum_{i=1}^{m} \lambda_{i}^{} \nabla g_{i}\left(\mathrm{x}^{}\right)+\sum_{j=1}^{p} \mu_{j}^{} \nabla h_{j}\left(\mathrm{x}^{}\right) = 0 \ \mu_{j}^{} \geq 0, \ \forall j=1,2, \cdots, p \ \mu_{j}^{}=0, \ \forall j \notin J\left(\mathrm{x}^{}\right)
$$
where $J(\mathbb x^∗)$ is the index set of active constraints at $\mathbb x^∗$. Let
$$
{\qquad H_{L}\left(\mathrm{x}^{}\right) =H_{f}\left(\mathrm{x}^{}\right)+\sum_{i=1}^{m} \lambda_{i}^{} H_{g_{i}}\left(\mathrm{x}^{}\right)+\sum_{j=1}^{p} \mu_{j}^{} H_{h_{j}}\left(\mathrm{x}^{}\right)}
$$
suppose
$$
{\mathrm{y}^{T} H_{L}\left(\mathrm{x}^{}\right) \mathrm{y} > 0}, \forall \mathbb y \in T(\mathbb x^) - {0}
$$
where $T(\mathbb x^*)$ is tangent space. $\mathbb x^*$ is a strict local minimizer.

steps:

1. verify it’s KKT point.
2. verify it satisfy the second order sufficient condition
   1. Hessian matrix
   2. $Z(\mathbf x^*)$
   3. Determine definiteness

5.4 KKT for constrained convex programming problems

For a convex problem, a feasible point $x^∗$ is a KKT point implies it is a global minimizer.
$$
\begin{array}{ll}{\min } & {f(\mathrm{x})} \ {\text { s.t. }} & {g_{i}(\mathrm{x}) :=\mathbf{a}{i}^{T} \mathrm{x}-b{i}=0, \quad i=1, \ldots, m} \ {} & {h_{j}(\mathrm{x}) \leq 0, \quad j=1, \ldots, p}\end{array}
$$
where $f, h_j : \mathbb{R}^n \rightarrow \mathbb{R}$ are convex function.

KKT point is an optimal solution under convexity

but a global minimizer of a convex program may not be a KKT point.

With regularity condition, a global minimizer is a KKT point. For convex programming problem with at least one inequality constraints, the Slater’s condition ensures that a global minimizer is a KKT point.

slater’s condition: there exists $\hat{\mathbb x} ∈ \mathbb R^n$ such that $g_i(\hat{\mathbb x}) = 0, ∀ i = 1,\cdots, m$ and $h_j(\hat{\mathbb x}) < 0, ∀ j = 1, . . . , p$.

 Slater's condition states that the feasible region must have an [interior point](https://en.wikipedia.org/wiki/Interior_(topology)).

5.4.1 Linear equality constrained convex program

Theorem 5.5. (Linear equality constrained convex program)

Consider the following linear equality constrained convex NLP:
$$
\begin{array}{rl}
\text{(ECP)} &
\begin{array}{l}
{\min f(\mathbb{x})} \
\text{s.t. } \mathbf A \mathbb x = \mathbb b
\end{array}
\end{array}
$$
where $\mathbf A$ is an $m × n$ matrix whose $i$-row is $\mathbb a_i^T$ and $f : \mathbb R^n → \mathbb R$ is a differentiable convex function. Suppose the feasible region $S$ is non-empty. Then a point $x^∗ ∈ S$ is a KKT point if and only if $x^∗$ is a global minimizer of $f$ on $S$.

KKT point $\iff$ global minimizer

==Note: no regularity or Slater’s condition is needed.==

Facts:

1. $\mathbb x \in S \iff \mathbb x = \mathbb x^* + \mathbb z$ for some $\mathbb z \in \operatorname{Null}(A)$. 【space of x】
2. $\mathbb y^T \mathbb z = 0$, $\forall \mathbb z \in \operatorname{Null}(\mathbf A) \iff \exist \lambda^* \in \mathbb R^m$ s.t. $\mathbb y+ \mathbf A^T \lambda^*=0$.

5.4.2 Linear & Convex quadratic programming problems

1. Linear programming
   $$
   \begin{array}{rl}{\min } & {f(\mathrm{x}) :=\mathrm{c}^{T} \mathrm{x}} \ {(\mathrm{LP}) \quad \text { s.t. }} & {\mathrm{b}-\mathrm{A} \mathrm{x}=0} \ {} & {\mathrm{x} \geq 0}\end{array}
   $$
   where $\mathbf A$ is $m\times n$, $\mathbb b\in \mathbb R^m$, $\mathbb a_i^T$ is $i$th row of $\mathbf A$.

   KKT conditions are:
   $$
   \begin{array}{l}{[1] \quad \mathrm{c}-\mathrm{A}^{T} \lambda-\mu=0} \ {[2] \quad \mathrm{b}-\mathrm{Ax}=0} \ {[3] \quad \mu \geq 0, \mathrm{x} \geq 0, \mu \circ \mathrm{x}=0}\end{array}
   $$
   where
   $$
   \mu \circ \mathrm{x} :=\left[\begin{array}{c}{\mu_{1} x_{1}} \ {\mu_{2} x_{2}} \ {\vdots} \ {\mu_{n} x_{n}}\end{array}\right]
   $$

2. Convex quadratic programming
   $$
   \begin{array}{rl}{\min } & {f(\mathbf{x}) :=\frac{1}{2} \mathbf{x}^{T} \mathbf{Q} \mathbf{x}+\mathbf{c}^{T} \mathbf{x}} \ {(\mathrm{QP})\quad \text { s.t. }} & {\mathbf{A} \mathbf{x}-\mathbf{b} \leq \mathbf{0}} \ {} & {\mathbf{x} \geq \mathbf{0}, \mathbf{x} \in \mathbb{R}^{n}}\end{array}
   $$
   where $\mathbf Q$ is positive semidefinite, $\mathbf A$ is $m\times n$, $\mathbb b\in \mathbb R^m$, $\mathbb a_i^T$ is $i$th row of $\mathbf A$.

   KKT conditions are:
   $$
   \begin{array}{l}{[1] \quad \mathrm{Qx+c}+\mathrm{A}^{T} \mu-\hat\mu=0} \
   {[2] \quad \mu \geq 0,\ \mathrm{Ax} \leq \mathbb b,\ \mu \circ \mathrm{(Ax-b)}=0}\
   {[2] \quad \hat\mu \geq 0,\ \mathrm{x} \geq 0,\ \hat\mu \circ \mathrm{x}=0}\
   \end{array}
   $$
   Let $\mathbb z = \mathrm{b-Ax}$, rewriteen:
   $$
   \begin{array}{c}
   {\mathrm{Qx+c}+\mathrm{A}^{T} \mu-\hat\mu=0} \
   {\mathrm{Ax+z}=\mathbb b} \
   {\mu \circ \mathrm{z}=0}\
   {\hat\mu \circ \mathrm{x}=0}\
   {\mu, \hat\mu, \mathbb x, \mathbb z \geq 0}.
   \end{array}
   $$
   Example:

   Sparse Regression Problem: $\frac{1}{2} | Ax-b|^2 + \rho |x|_1$ where $\rho > 0$.

   Reformulated as:
   $$
   \begin{array}{ll}{\min } & {f\left(x, u^{(1)}, u^{(2)}\right) :=\frac{1}{2}|A x-b|^{2}+\rho\left\langle e, u^{(1)}+u^{(2)}\right\rangle} \ {\text { s.t. }} & { g\left(x, u^{(1)}, u^{(2)}\right) :=x-u^{(1)}+u^{(2)}=0} \ {} & {h_{1}\left(x, u^{(1)}, u^{(2)}\right) :=-u^{(1)} \leq 0} \ {} & {h_{2}\left(x, u^{(1)}, u^{(2)}\right) :=-u^{(2)} \leq 0}\end{array}
   $$
   KKT conditions:
   $$
   \begin{array}{c}
   {\left(\begin{array}{c}{A^{T}(A x-b)} \ {\rho e} \ {\rho e}\end{array}\right)+\left(\begin{array}{c}{I} \ {-I} \ {I}\end{array}\right) \lambda+\left(\begin{array}{c}{0} \ {-I} \ {0}\end{array}\right) \mu^{(1)}+\left(\begin{array}{c}{0} \ {0} \ {-I}\end{array}\right) \mu^{(2)}=\left(\begin{array}{c}{0} \ {0} \ {0}\end{array}\right)} \
   {\qquad \begin{array}{c}{x-u^{(1)}+u^{(2)}=0} \
   {\mu^{(1)} \circ u^{(2)} = 0, \quad \mu^{(2)} \circ u^{(2)}=0} \
   {u^{(1)} , u^{(2)}, \mu^{(1)}, \mu^{(2)} \geq 0}
   \end{array}}\end{array}
   $$
   eliminated the system, we have:
   $$
   \begin{array}{c}
   {u^{T}(A x-b)+\lambda=0} \
   {-\rho e \leq \lambda \leq \rho e} \
   {(\rho e-\lambda) \circ \max {x, 0}=0, \quad(\rho e+\lambda) \circ \max {-x, 0}=0} \
   \iff \lambda_i \in \begin{cases} { \rho } & \text{if } x_i>0, \ [-\rho, \rho] \quad & \text{if } x_i = 0 \ { -\rho } \quad & \text{if } x_i < 0 \end{cases} \quad i=1,\cdots, n.
   \end{array}
   $$

5.5 Proof of KKT 1st necessary conditions

via the Penalty Approach

5.6 Summary